题目内容
有下列几种说法：①角平分线上的点到角两边的距离相等；②顺次连结矩形四边中点
得到的四边形是菱形；③等腰梯形的底角相等；④平行四边形是中心对称图形．其中正确
的有（ ）
| A．4个 | B．3个 | C．2个 | D．1个 |
B
解析试题分析：①正确，符合角平分线的性质；
②正确，连接AC、BD，在△ABD中，∵AH=HD，AE=EB，∴EH=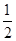
BD，同理FG=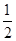BD，HG=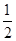AC，EF=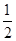AC，又∵在矩形ABCD中，AC=BD，∴EH=HG=GF=FE，∴四边形EFGH为菱形．符合等腰三角形的轴对称性质；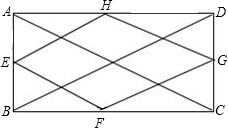
③错误，没说清是不是同一底上的角；
④正确，符合平行四边形的中心对称性质．故选B．
考点：中心对称图形；角平分线的性质；等腰梯形的性质．
点评：本题要求综合了解中心对称图形与轴对称图形的概念，角平分线和等腰梯形的性质，难度不大．
练习册系列答案
名校课堂系列答案
相关题目