题目内容
【题目】如图，在数轴上有两点A、B，点A表示的数是8，点B在点A的左侧，且AB=14，动点P从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．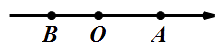
（1）写出数轴上点B表示的数： ；点P表示的数用含t的代数式表示为 ．
（2）动点Q从点B出发沿数轴向左匀速运动，速度是点P速度的一半，动点P、Q同时出发，问点P运动多少秒后与点Q的距离为2个单位？
（3）若点M为线段AP的中点，点N为线段BP的中点，在点P的运动过程中，线段MN的长度是否会发生变化？若变化，请说明理由；若不变，求出线段MN的长．
【答案】
（1）解：8-14=-6；因此B点为-6；故答案为:-6,解：因为时间为t,则点P所移动距离为4t,因此点P为8－4t ;故答案为：8-4t
（2）解：由题意得，Q 的速度为4÷2=2（秒）则点Q为-6-2t，又点P为8-4t；
所以①P在Q的右侧时
8-4t-（-2t-6）=2
解得x=6
②P在Q左侧时
-2t-6-（8-4t）=2
解得x=8
答：动点P、Q同时出发，问点P运动6或8秒后与点Q的距离为2个单位.
故答案为：6或8秒
（3）解：①当P在A,B之间时，线段AP=8-（8-4t）=4t；线段BP=8-4t-（-6）=14-4t
因点M为线段AP的中点，点N为线段BP的中点
所以MP=
AP=2t；NP=BP=7-2t
MN=MP+NP=2t+7-2t=7
②当P在P的左边时线段AP=8-（8-4t）=4t；线段BP=（-6）-（8-4t）=4t-14
因点M为线段AP的中点，点N为线段BP的中点
所以MP=AP=2t；NP=BP=2t-7
MN=MP-NP=2t-(2t-7)=7
因此在点P的运动过程中，线段MN的长度不变， MN=7
【解析】（1）①由数轴上两点之间距离的规律易得B的值为8-14=16；
②因为时间为t，则点P所移动距离为4t，因此易得P为8-4t
（2）由题易得：Q 的速度为4÷2=2（秒）则点Q为-6-2t，又点P为8-4t；分别讨论P在Q左侧或右侧的情况，由此列方程，易得结果为6或8秒；
（3）结合（1）（2）易得当P在AB间以及P在B左边时的两种情况；当P在A,B之间时，线段AP=8-（8-4t）=4t；线段BP=8-4t-（-6）=14-4t；当P在P的左边时线段AP=8-（8-4t）=4t；线段BP=（-6）-（8-4t）=4t-14；利用中点性质，易得结果不变，为7.
