题目内容
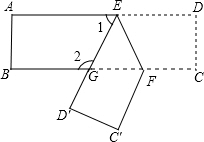
如图把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D、C分别在M 、N的位置上，若∠FEG=55°，则∠1=____ °，∠2=____ °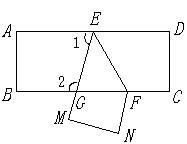
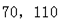
由平行线的性质知∠DEF=∠EFB=55°，由题意知∠GEF=∠DEF=55°，则可求得∠2=∠GED=110°．由邻补角的性质可求得∠1的值．
解：
∵AD∥BC
∴∠DEF=∠EFB=55°（2分）
由对称性知∠GEF=∠DEF
∴∠GEF=55°
∴∠GED=110°
∴∠1=180°-110°=70°
∴∠2=∠GED=110°
本题考查了翻折的性质，对应角相等及平行线的性质、邻补角的性质．
解：
∵AD∥BC
∴∠DEF=∠EFB=55°（2分）
由对称性知∠GEF=∠DEF
∴∠GEF=55°
∴∠GED=110°
∴∠1=180°-110°=70°
∴∠2=∠GED=110°
本题考查了翻折的性质，对应角相等及平行线的性质、邻补角的性质．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
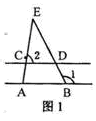
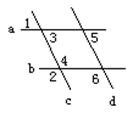
的补角比这个角的余角大多少度？
