题目内容
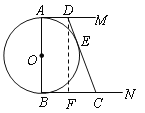
【题目】如图,⊙O 的直径AB=2,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN于C.设![]() .
.
(1)求证: ![]() ;(2)求
;(2)求![]() 关于
关于![]() 的关系式.
的关系式.

【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)由AB是直径,AM、BN是切线,得到AM⊥AB,BN⊥AB,根据垂直于同一条直线的两直线平行即可得到结论;
(2)过点D作 DF⊥BC于F,则AB∥DF,由(1)AM∥BN,得到四边形ABFD为矩形,于是得到DF=AB=2,BF=AD=x,根据切线长定理得DE=DA=x,CE=CB=y.根据勾股定理即可得到结果;
试题解析:
证明:∵AB是直径,AM、BN是切线,
∴![]() ,
,
∴![]() .
.
(2)解:过点D作 ![]() 于F,则
于F,则![]() .
.
由(1)![]() ,
,
∴四边形![]() 为矩形.
为矩形.
∴![]() ,
, ![]() .
.
∵DE、DA,CE、CB都是切线,
∴根据切线长定理,得![]() ,
, ![]() .
.
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
化简,得![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目