题目内容
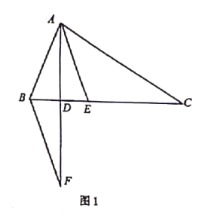
【题目】如图,在ABCD中,AB=6a,BC=6b,∠D=60°,点E、F、G、H分别在ABCD各边上,且BE=DG=![]() AE,CF=AH=
AE,CF=AH=![]() BF.
BF.
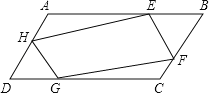
(1)求证:四边形EFGH是平行四边形;
(2)若四边形EFGH是菱形,求![]() 的值;
的值;
(3)四边形EFGH能为正方形吗?若能,请直接写出a、b的值;若不能,请说明理由.
【答案】(1)见解析;(2)![]() ;(3)不能,理由见解析
;(3)不能,理由见解析
【解析】
(1)证明△DGH≌△BEF,可得GH=EF,同理证得△AEH≌△CGF,可得EH=GF,则结论得证;
(2)过H,F作HP⊥CD,FQ⊥CD,交直线CD于P、Q,可得∠DHP=∠CFQ=30°,求出DP=2b,FQ=b,则PG=2a﹣2b,QG=b+4a,由PG2+PH2=GQ2+FQ2,得出a、b的关系式12a2+16ab﹣12b2=0,可求得![]() ;
;
(3)可证明△PHG≌△QGF,得出HP=GQ,PG=QF,则2![]() b=4a+b,2a﹣2b=
b=4a+b,2a﹣2b=![]() ,解出a=0,b=0,故四边形EFGH不能是正方形.
,解出a=0,b=0,故四边形EFGH不能是正方形.
(1)∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,AB=CD=6a,AD=BC=6b,
∵BE=![]() ,
,
∴AB=AE+![]() AE,
AE,
∴AE=4a,BE=DG=2a,CG=4a,
同理AH=CF=2b,DH=BF=4b,
∴
∴△DGH≌△BEF(SAS),
∴GH=EF,
同理△AEH≌△CGF(SAS),
∴EH=GF,
∴四边形EFGH是平行四边形;
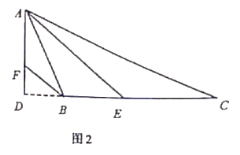
(2)如图,过H,F作HP⊥CD,FQ⊥CD,交直线CD于P,Q,

∵平行四边形ABCD中,AD∥BC,
∴∠D=∠BCQ=60°,
∴∠DHP=∠CFQ=30°,
∴DP=![]() =2b,CQ=
=2b,CQ=![]() =b,
=b,
∴PH=![]() =2
=2![]() b/span>,FQ=
b/span>,FQ=![]() =
=![]() b,
b,
∴PG=DG﹣DP=2a﹣2b,QG=QC+CG=b+4a,
∵四边形EFGH是菱形,
∴GH=GF,
∴PG2+PH2=GQ2+FQ2,
∴![]() =
=![]() ,
,
化简得:12a2+16ab﹣12b2=0,
3b2﹣3a2=4ab,
两边同除以3ab,得![]() ;
;
(3)不能,理由如下:
若四边形EFGH是正方形,则HG=FG,∠HGF=90°,
∴∠HGP+∠FGQ=90°,
∵HP⊥CD,
∴∠HGP+∠GHP=90°,
∴∠FGQ=∠GHP,
在△PHG和△QGF中,
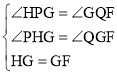 ,
,
∴△PHG≌△QGF(AAS),
∴HP=GQ,PG=QF,
∴2![]() b=4a+b,2a﹣2b=
b=4a+b,2a﹣2b=![]() ,
,
解得:a=0,b=0,
∴四边形EFGH不能是正方形.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案【题目】红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的 日销售量(件)与时间(天)的关系如下表:
时间(天) | 1 | 3 | 6 | 10 | 36 | … |
日销售量(件) | 94 | 90 | 84 | 76 | 24 | … |
未来40天内,前20天每天的价格y1(元/件)与t时间(天)的函数关系式为:y1=![]() t+25(1≤t≤20且t为整数);后20天每天的价格y2(原/件)与t时间(天)的函数关系式为:y2=—
t+25(1≤t≤20且t为整数);后20天每天的价格y2(原/件)与t时间(天)的函数关系式为:y2=—![]() t+40(21≤t≤40且t为整数).下面我们来研究 这种商品的有关问题.
t+40(21≤t≤40且t为整数).下面我们来研究 这种商品的有关问题.
(1)认真分析上表中的数量关系,利用学过的一次函数、二次函数 、反比例函数的知识确定一个满足这些数据之间的函数关系式;
(2)请预测未来40天中那一天的销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程,公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.