Question

【题目】(2016广东省深圳市第23题)如图，抛物线与轴交于A、B两点，且B（1 , 0）。

(1)、求抛物线的解析式和点A的坐标；

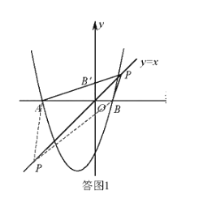
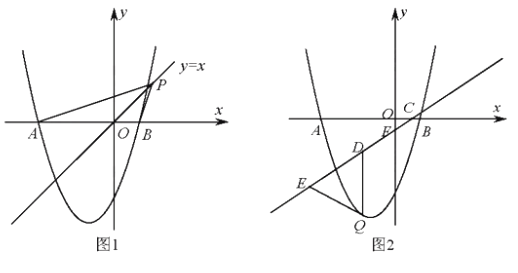
(2)、如图1，点P是直线上的动点，当直线平分∠APB时，求点P的坐标；

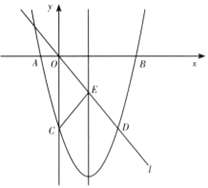
（3）如图2，已知直线 分别与轴 轴 交于C、F两点。点Q是直线CF下方的抛物线上的一个动点，过点Q作 轴的平行线，交直线CF于点D，点E在线段CD的延长线上，连接QE。问以QD为腰的等腰△QDE的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由。

Answer 1

【答案】(1)、y=x+2x-3 ,A(-3,0)；(2)、(，)；(3)、△QDE的面积最大值为.

【解析】

试题分析：(1)、把点B的坐标代入解析式得出函数解析式和点A的坐标；(2)、若y=x平分∠APB，则∠APO=∠BPO，若P点在x轴上方，PA与y轴交于点，从而得出△≌△OPB，从而得出点P的坐标；当点P在x轴下方时，不成立；(3)、作QH⊥CF，根据直线CF的解析式得出点C和点F的坐标，求出tan∠OFC的值，△QDE是以DQ为腰的等腰三角形，根据DQ=DE得出函数解析式，则当DQ=QE时则△DEQ的面积比DQ=DE时大，然后设点Q的坐标，求出函数解析式得出最大值.

试题解析：(1)、把B（1,0）代入y=ax+2x-3 得a+2-3=0,解得a=1

∴y=x+2x-3 ,A(-3,0)

(2)、若y=x平分∠APB，则∠APO=∠BPO

如答图1，若P点在x轴上方，PA与y轴交于点 ∵∠POB=∠PO=45°，∠APO=∠BPO，PO=PO

∴△≌△OPB ∴=1, ∴PA: y=3x+1 ∴

若P点在x轴下方时， 综上所述，点P的坐标为

(3)、如图2，作QH⊥CF， CF:y=，C(，0),F(0，) tan∠OFC=

DQ∥y轴 ∠QDH=∠MFD=∠OFC tan∠HDQ=

不妨记DQ=1,则DH=,HQ= △QDE是以DQ为腰的等腰三角形

若DQ=DE,则

若DQ=QE,则

＜ 当DQ=QE时则△DEQ的面积比DQ=DE时大

设Q 当DQ=t=

以QD为腰的等腰△QDE的面积最大值为