题目内容
【题目】在ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.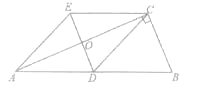
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析: (1)由DE∥BC,CE∥AB,可证得四边形DBCE是平行四边形,又由△ABC中,∠BCA=90°,CD是边AB上的中线,根据直角三角形斜边的中线等于斜边的一半,可得CD=AD=BD=CE,然后由CE∥AB,证得四边形ADCE平行四边形的性质,继而证得四边形ADCE是菱形;
(2)首先过点C作CF⊥AB于点F,由(1)可知,BC=DE,设BC=x,则AC=2x,然后由勾股定理求得AB,再由三角形的面积,求得CF的长,由勾股定理即可求得CD的长,继而求得答案.
试题解析:
(1)∵DE∥BC,EC∥AB,
∴四边形DBCE是平行四边形.
∴EC∥DB,且EC=DB.
在Rt△ABC中,CD为AB边上的中线,
∴AD=DB=CD.
∴EC=AD.
∴四边形ADCE是平行四边形.
∵ED∥BC.
∴∠AOD=∠ACB.
∵∠ACB=90°,
∴∠AOD=∠ACB=90°.∴平行四边形ADCE是菱形;
(2)过点C作CF⊥AB于点F,
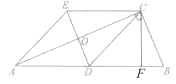
由(1)可知,BC=DE,设BC=x,则AC=2x,
在Rt△ABC中,AB= ![]() , CD=
, CD= ![]() AB=
AB= ![]() ,
,
因为 ![]() AB·CF=
AB·CF= ![]() AC·BC,
AC·BC,
所以CF= ![]() x,
x,
则sin∠CDB= ![]() =
= ![]()

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目



