Question

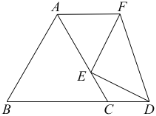
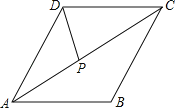
【题目】如图，菱形ABCD的边长为6，∠B＝120°．点P是对角线AC上一点（不与端点A重合），则AP+PD的最小值为_____．

Answer 1

【答案】3

【解析】

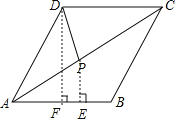
过点P作PE⊥AB于点E，过点D作DF⊥AB于点F，根据四边形ABCD是菱形，且∠B＝120°，∠DAC＝∠CAB＝30°，可得PE＝AP，当点D，P，E三点共线且DE⊥AB时，PE+DP的值最小，最小值为DF的长，根据勾股定理即可求解．

解：如图，过点P作PE⊥AB于点E，过点D作DF⊥AB于点F,

∵四边形ABCD是菱形，且∠B＝120°,

∴∠DAC＝∠CAB＝30°,

∴PE＝AP;

∵∠DAF＝60°,

∴∠ADF＝30°,

∴AF＝AD＝×6＝3;

∴DF＝3;

∵AP+PD＝PE+PD,

∴当点D，P，E三点共线且DE⊥AB时,

PE+DP的值最小，最小值为DF的长,

∴AP+PD的最小值为3.

故答案为：3.