题目内容
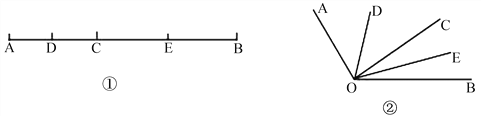
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一个动点,点D、E分别是AC和BC的中点.
(1)若点C恰好是AB的中点,则DE= cm;若AC=4cm,则DE= cm;
(2)随着C点位置的改变,DE的长是否会改变?如果改变,请说明原因;如果不变,请求出DE的长;
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE的度数与射线OC的位置无关.
【答案】(1)6,6;(2)DE的长不会改变,理由见解析;(3)理由见解析.
【解析】试题分析:(1)由AB=12cm,点D、E分别是AC和BC的中点,即可推出DE=![]() (AC+BC)=
(AC+BC)= ![]() AB;由AC=4cm,AB=12cm,即可推出BC=8cm,然后根据点D、E分别是AC和BC的中点,即可推出AD=DC,BE=EC,由此即可得到DE的长度;
AB;由AC=4cm,AB=12cm,即可推出BC=8cm,然后根据点D、E分别是AC和BC的中点,即可推出AD=DC,BE=EC,由此即可得到DE的长度;
(2)由(1)知,C点位置的改变后,仍有DE=CD+CE=![]() (AC+BC)=
(AC+BC)= ![]() AB,所以DE的长度不会改变;
AB,所以DE的长度不会改变;
(3)由若OD、OE分别平分∠AOC和∠BOC,即可推出∠DOE=∠DOC+∠COE=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)= ![]() ∠AOB,继而可得到答案.
∠AOB,继而可得到答案.
解:(1)若点C恰好是AB的中点,则DE= 6 cm;
若AC=4cm,则DE= 6 cm;
(2)DE的长不会改变,理由如下:
∵ 点D是线段AC的中点
∴ ![]()
∵ 点E是线段BC的中点
∴ ![]()
∴ DE = DC+CE ![]()
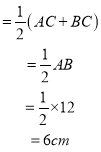
∴ DE的长不会改变;
(3)∵ OD平分∠AOC, OE平分∠BOC
∴![]() ,
, ![]()
∴![]()
![]()
![]()
![]()
![]()
![]()
∴∠DOE的度数与射线OC的位置无关.

【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?
