Question

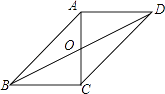
【题目】如图，O为矩形ABCD对角线的交点，DE∥AC，CE∥BD．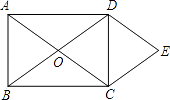
（1）试判断四边形OCED的形状，并说明理由；
（2）若AB=6，BC=8，求四边形OCED的面积．

Answer 1

【答案】
（1）解：四边形OCED是菱形．

∵DE∥AC，CE∥BD，

∴四边形OCED是平行四边形，

又在矩形ABCD中，OC=OD，

∴四边形OCED是菱形

（2）解：连接OE．由菱形OCED得：CD⊥OE，

又∵BC⊥CD，

∴OE∥BC（在同一平面内，垂直于同一条直线的两直线平行），

又∵CE∥BD，

∴四边形BCEO是平行四边形；

∴OE=BC=8

∴S四边形OCED= OECD= ×8×6=24．

【解析】（1）首先可根据DE∥AC、CE∥BD判定四边形ODEC是平行四边形，然后根据矩形的性质：矩形的对角线相等且互相平分，可得OC=OD，由此可判定四边形OCED是菱形．（2）连接OE，通过证四边形BOEC是平行四边形，得OE=BC；根据菱形的面积是对角线乘积的一半，可求得四边形ODEC的面积．