题目内容
(2004•沈阳)已知△ABC中,∠C=90°,AC=3,BC=4,分别以A、C为圆心作⊙A、⊙C,且⊙C与直线AB不相交,⊙A与⊙C相切.设⊙A的半径为r,那么r的取值范围是 .
【答案】分析:根据勾股定理得AB=5,⊙C与直线AB不相交,有可能相切或者相离,从而求得⊙C的半径的取值范围;再根据两圆相切,求得r的取值范围.
解答:解:根据勾股定理,得:AB=5,
根据题意,知⊙C与直线AB相切或相离,
相切时,⊙C的半径即是AB上的高,即为2.4,
所以⊙C的半径的取值范围是小于或等于2.4;
又⊙A与⊙C相切,则可能内切,也可能外切,
当两圆外切时,则0.6≤r<3,
当两圆内切时,则3<r≤5.4.
∴0.6≤r<3或3<r≤5.4.
点评:此题综合考查了直线和圆以及两圆的位置关系与数量之间的联系.本题需注意两圆相切,应分内切和外切两种情况.
解答:解:根据勾股定理,得:AB=5,
根据题意,知⊙C与直线AB相切或相离,
相切时,⊙C的半径即是AB上的高,即为2.4,
所以⊙C的半径的取值范围是小于或等于2.4;
又⊙A与⊙C相切,则可能内切,也可能外切,
当两圆外切时,则0.6≤r<3,
当两圆内切时,则3<r≤5.4.
∴0.6≤r<3或3<r≤5.4.
点评:此题综合考查了直线和圆以及两圆的位置关系与数量之间的联系.本题需注意两圆相切,应分内切和外切两种情况.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
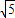
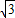
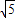
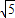

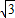
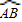 的度数为70°,过点A的直线AC与⊙O相切,则弦切角∠BAC的度数为 .
的度数为70°,过点A的直线AC与⊙O相切,则弦切角∠BAC的度数为 .