题目内容
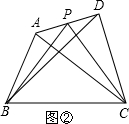
提出问题:如图,在“儿童节”前夕,小明和小华分别获得一块分布均匀且形状为等腰梯形和直角梯形的蛋糕(AD∥BC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将自己的这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).背景介绍:这条分割直线既平分了梯形的面积,又平分了梯形的周长,我们称这条线为梯形的“等分积周线”.
【小题1】小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中作出这条“等分积周线”,从而平分蛋糕.

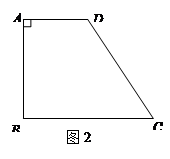
【小题2】小华觉得小明的方法很好,所以模仿着在自己的蛋糕(图2)中画了一条直线EF分别交AD、BC于点E、F.你觉得小华会成功吗?如能成功,说出确定的方法;
 如不能成功,请说明理由
如不能成功,请说明理由【小题3】通过上面的实践,你一定有了更深刻的认识.若图2中AD∥BC,∠A=90°,AD<BC,AB="4" cm,BC ="6" cm,CD= 5cm.请你找出梯形ABCD的所有“等分积周线”,并简要的说明确定的方法.
【小题1】作线段AD(或BC)的中垂线即可
【小题2】小华不会成功.直线平分梯形ABCD面积,则
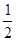 (AE+BF)AB=
(AE+BF)AB=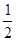 (ED+CF)AB
(ED+CF)AB∴AE+BF = ED+CF,又∵AB<CD,∴此时AE+BF+ AB<ED+CF+ CD
∴小华不可能成功 …………3分
【小题3】可求得:S梯形ABCD=18,C梯形ABCD=18,
由(2)可知直线分别交AD、BC于点E、F时不可能,只要分以下几种情况:
① 当直线分别交AD、AB于E、F时
有 S△AEF≤S△ABD,又∵S△ABD=6<9,∴不可能
同理,当直线分别交AD、CD于E、F时S△AEF≤S△ACD<9,
∴不可能 …………4分
②当直线分别交AB、BC于E、F时
设BE=x, 则BF=9?x
由直线平分梯形面积得: x(9?x)=9
求得:x1=3,x2=6>4(舍去)
∴BE=3 …………6分
③当直线分别交CD、BC于E、F时
设CE="x," 可得:S△ECF=××(9?x)=9
2 x2-18 x+45=0
此方程无解,∴不可能…………8分
④当直线分别交AB、CD于、 E、F时
设CF=x,可得:SBFEC=×(3?)(6?)+= 9
∴ x1=0, 与②同
x2="5" ,BF=?2,舍去 …………10分
综上所述,符合条件的直线共有一条.解析:
略

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
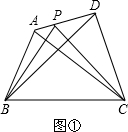
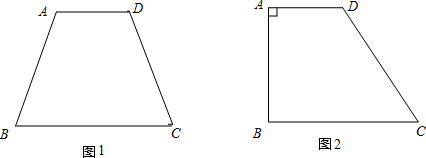
 (2012•浦口区一模)提出问题:
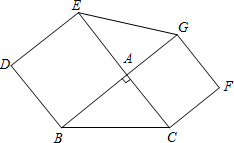
(2012•浦口区一模)提出问题: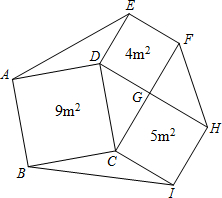 ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
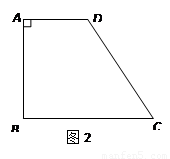
 如不能成功,请说明理由
如不能成功,请说明理由