题目内容
 如图,∠AOB是直角,OD平∠BOC,OE平分∠AOC.
如图,∠AOB是直角,OD平∠BOC,OE平分∠AOC.求:(1)∠EOD的度数.
(2)当OC在∠A0B内绕点O转动时,∠DOE的值会不会改变?
分析:(1)由于∠AOB是直角,OD平∠BOC,OE平分∠AOC,那么利用角平分线有∠COD=
∠BOC,∠COE=
∠AOC,再利用等式性质,可得∠COD+∠COE=
(∠BOC+∠AOC),即可求∠DOE;
(2)由(1)的结论可知∠DOE=
∠AOB,而∠AOB的度数不变,则∠DOE就不变,也就是OC在∠A0B内绕点O转动时,∠DOE的值不会改变.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)的结论可知∠DOE=
| 1 |
| 2 |
解答:解:(1)∵∠AOB是直角,OD平∠BOC,OE平分∠AOC.
∴∠COD=
∠BOC,∠COE=
∠AOC,
∴∠COD+∠COE=
(∠BOC+∠AOC),
即∠DOE=∠AOB=
×90°=45°;
(2)当OC在∠A0B内绕点O转动时,∠DOE的值不会改变.
∵由(1)知∠DOE=
∠AOB,而∠AOB的度数不变,则∠DOE就不变.
∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠COD+∠COE=
| 1 |
| 2 |
即∠DOE=∠AOB=
| 1 |
| 2 |
(2)当OC在∠A0B内绕点O转动时,∠DOE的值不会改变.
∵由(1)知∠DOE=
| 1 |
| 2 |
点评:本题考查了角的计算、角平分线的定义、等式的性质.

练习册系列答案
相关题目
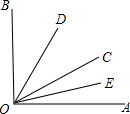
 25、如图,∠AOB是直角,∠COD也是直角,若∠AOC=α,则∠BOD等于( )
25、如图,∠AOB是直角,∠COD也是直角,若∠AOC=α,则∠BOD等于( )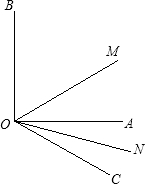 已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线. 如图,∠AOB是直角,OB平分∠COD,∠COD=40°,则∠AOD=
如图,∠AOB是直角,OB平分∠COD,∠COD=40°,则∠AOD=