题目内容
如图，∠AOB是直角，OD平分∠BOC，OE平分∠AOC，求∠EOD的度数．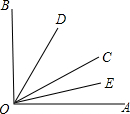
分析：根据角平分线的性质，转化相等关系，求出∠EOD的度数．
解答：解：∵OD平分∠BOC，
∴∠BOD=∠DOC，
∵OE平分∠AOC，
∴∠COE=∠EOA，
又∵∠AOB是直角，
∴∠BOC+∠COA=90°，
∴∠DOC+∠COE=
×90°=45°．
∴∠EOD=45°．
故答案为45°．
∴∠BOD=∠DOC，
∵OE平分∠AOC，
∴∠COE=∠EOA，
又∵∠AOB是直角，
∴∠BOC+∠COA=90°，
∴∠DOC+∠COE=
| 1 |
| 2 |
∴∠EOD=45°．
故答案为45°．
点评：根据角平分线定义得出所求角与已知角的关系转化求解．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
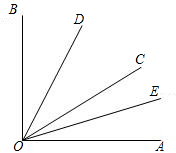如图，∠AOB是直角，OD平∠BOC，OE平分∠AOC．
25、如图，∠AOB是直角，∠COD也是直角，若∠AOC=α，则∠BOD等于（ ）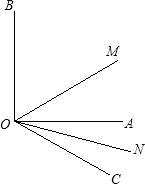
已知：如图，∠AOB是直角，∠AOC=40°，ON是∠AOC的平分线，OM是∠BOC的平分线．
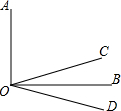如图，∠AOB是直角，OB平分∠COD，∠COD=40°，则∠AOD=