��Ŀ����
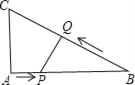
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y=ax2+bx+c��ͼ����A����1��0����B��0����![]() ����C��2��0������Գ�����x�ύ�ڵ�D
����C��2��0������Գ�����x�ύ�ڵ�D
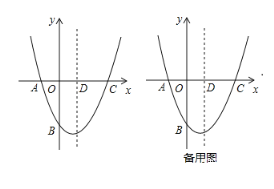
��1������κ����ı���ʽ���䶥�����ꣻ
��2����PΪy���ϵ�һ�����㣬����PD����![]() PB+PD����Сֵ��
PB+PD����Сֵ��
��3��M��x��t��Ϊ�����߶Գ�����һ����
����ƽ���ڴ��ڵ�N��ʹ����A��B��M��NΪ������ı���Ϊ���Σ��������ĵ�N������ ������
������MA��MB������AMB��С��60������t��ȡֵ��Χ��
���𰸡���1�������߽���ʽΪy=![]() x2��
x2��![]() x��
x��![]() ���������꣨
���������꣨![]() ����
����![]() ������2��
������2��![]() PB+PD����СֵΪ
PB+PD����СֵΪ![]() ����3����5;��ȡֵ��Χ��
����3����5;��ȡֵ��Χ��![]()
��������
���κ����ı���ʽ�����ַ�������������Կ����ö���ʽ�Լ�����ʽ������Щ����һ����ݱߵĹ�ϵ�ó���ABO=30��dz���Ҫ��������ֱ���������У�30�����Եı���б�ߵ�һ�����Ҫ��ı�ת�����ٸ��ݵ㵽ֱ�ߴ��߶���������Сֵ��������ABMN������Σ�ֻ��AB�Ƕ��㣬����Ҫ����AB���ڱ��ǶԽ��ߣ����һ����Բ��֪ʶ���ϣ���һ�����Ѷȣ���Ҫ���ݡ�ABO=30�㣬AB=2�Ƕ�ֵ����AB�Ĵ�ֱƽ������y��Ľ���ΪԲ��F����FAΪ�뾶����AB���Ե�Բ�ܽ�Ϊ60�㣬��Գ�����������㼴Ϊt��ȡֵ��Χ.
��1������һ������κ����ı���ʽΪ![]() ��B��0��-
��B��0��-![]() ��������
��������![]()
��![]()
�ඥ������Ϊ![]()
��������Ҳ����������ʽ��![]() ����������߶���ʽ��
����������߶���ʽ��![]() ����������á�
����������á�
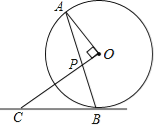
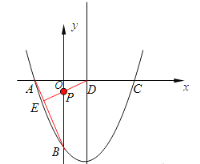
��ͼ����P����DE��AB��E�㣬��������֪��ABO=30��.
��![]()
��![]()
Ҫʹ![]() ��С��ֻ��ҪD��P��E���ߣ����Թ�D����DE��AB��E�㣬��y��Ľ��㼴ΪP��.
��С��ֻ��ҪD��P��E���ߣ����Թ�D����DE��AB��E�㣬��y��Ľ��㼴ΪP��.
��������֪����ADE=��ABO=30�㣬![]() ,
,
![]()
����A��B��M��NΪ������ı���Ϊ���Σ������������������֪��AB=2��
��ABΪ�����εıߣ���ΪMΪ�����߶Գ����ϵ�һ�㣬���ֱ���A��BΪ���㣬AB�ij�Ϊ�뾶��Բ��Գ���Ľ��㼴ΪM�㣬������M�����ĸ�����ͼ
��ABΪ���εĶԽ��ߣ��������ε����ʣ���AB�Ĵ�ֱƽ������Գ���Ľ��㼴ΪM��.
����������������M����5�������Զ�Ӧ��N����5��.
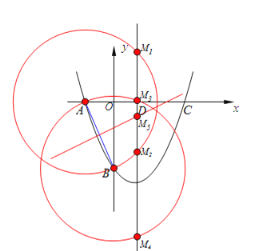
����ͼ����AB�Ĵ�ֱƽ���ߣ���y�ύ��F�㡣
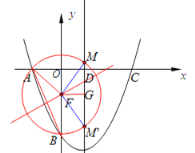
������֪��AB=2����BAF=��ABO=30�㣬��AFB=120��
����FΪԲ�ģ�AF�ij�Ϊ�뾶��Բ���Գ�����M��M'�㣬���AMB=��AM'B=![]() ��AFB=60��
��AFB=60��
�ߡ�BAF=��ABO=30�㣬OA=1
���FAO=30�㣬AF=![]() =FM=FM'��OF=
=FM=FM'��OF=![]() ����F����FG��MM'��G�㣬��֪FG=
����F����FG��MM'��G�㣬��֪FG=![]()
��![]() ���֡�G
���֡�G![]()
��M��![]() ��M'
��M'![]()
��![]()
����������M![]() ��M����F
��M����F![]() �ľ���d=AF=
�ľ���d=AF=![]() Ҳ����ã�
Ҳ����ã�