题目内容
 如图,已知以AB为直径,O为圆心的半圆与直线MN相切于点C,∠A=28°.
如图,已知以AB为直径,O为圆心的半圆与直线MN相切于点C,∠A=28°.(1)求∠ACM的度数.
(2)若点A到直线MN的距离为6,直径AB的长为8,求弦AC的长.
分析:(1)连接OC,由于OC是切线,那么∠OCD=90°,又∠A=28°,OA=OC,易求∠ACO=28°,从而可求∠ACM;
(2)过点A作AD⊥MN垂足为D,连接BC,由于AB是直径,那么∠ACB=90°,而∠A=28°,易求∠ABC,从而有∠ABC=∠ACM,而∠ADC=∠ACB=90°,易证△ADC∽△ACB,再利用比例线段可求AC.
(2)过点A作AD⊥MN垂足为D,连接BC,由于AB是直径,那么∠ACB=90°,而∠A=28°,易求∠ABC,从而有∠ABC=∠ACM,而∠ADC=∠ACB=90°,易证△ADC∽△ACB,再利用比例线段可求AC.
解答:解:(1)连接OC,
∵MN是⊙O切线,
∴∠OCD=90°,
又∵∠A=28°,OA=OC,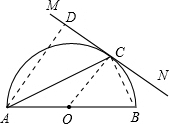
∴∠ACO=28°,
∴∠ACM=∠OCD-∠ACO=90°-28°=62°;
(2)过点A作AD⊥MN垂足为D,连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=28°,
∴ABC=62°,
∴∠ABC=∠ACM,
又∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴
=
,
∴6:AC=AC:8,
∴AC=4
.
∵MN是⊙O切线,
∴∠OCD=90°,
又∵∠A=28°,OA=OC,

∴∠ACO=28°,
∴∠ACM=∠OCD-∠ACO=90°-28°=62°;
(2)过点A作AD⊥MN垂足为D,连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=28°,
∴ABC=62°,
∴∠ABC=∠ACM,
又∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴
| AD |
| AC |
| AC |
| AB |
∴6:AC=AC:8,
∴AC=4
| 3 |
点评:本题考查了切线的性质、直径所对的圆周角等于90°、相似三角形的判定和性质.解题的关键是连接OC,并过A作AD⊥MN垂足为D,连接BC,构造等腰三角形、直角三角形以及平行线.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

 (2012•咸丰县二模)如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于( )
(2012•咸丰县二模)如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于( )
 如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于
如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于