题目内容
如图，∠ACB=∠ADB=90°，AC=AD，点E在AB上。
（1）试说明点A在∠CBD的平分线上；
（2）请你探索线段CE与DE的数量关系，并说明理由。
（1）试说明点A在∠CBD的平分线上；
（2）请你探索线段CE与DE的数量关系，并说明理由。
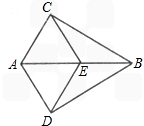
证明：（1）∵AB=AB，∠ACB=∠ADB=90°，AC=AD，
∴Rt△ACB≌Rt△ADB，
∴∠CBA=∠DBA，即点A在∠CBD的平分线上；
（2）CE=DE，
理由：由（1）知，∠CAB=∠DAB，
∵AC=AC，AE=AE，
∴△ACE≌△ADE，
∴CE=DE。
练习册系列答案
相关题目
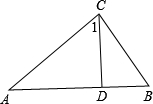如图，△ACB中，∠ACB=90°，∠1=∠B．
13、如图，∠ACB=90°，把Rt△ABC绕点A逆时针旋转90°得到Rt△AB1C1，若BC=1，AB=2，则∠CAB1的度数是
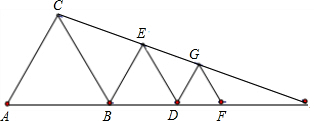如图，△ACB、△BDE和△DGF都是等边三角形，且点E、G在△ABC边AB的延长线上，设等边的面积分别为S1、S2、S3，若S1=9，S3=1，则S2=
如图，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于D，AD=5cm，DE=2.3cm，则BE的长为
已知：如图，∠ACB=∠DBC，根据图形条件，若增加一个条件