题目内容
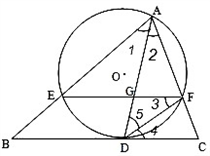
如图，△ABC中，∠BAC的平分线AD交BC于D，⊙O过点A，且和BC切于D，和AB、AC分别交于E、F．设EF交AD于G，连接DF．
（1）求证：EF∥BC；
（2）已知：DF=2，AG=3，则
=_________．
（1）求证：EF∥BC；
（2）已知：DF=2，AG=3，则
=_________．
解：（1）证明：∵⊙O切BC于D
∴∠4=∠2
又∵∠1=∠3，∠1=∠2
∴∠3=∠4
∴EF∥BC
（2）∵∠1=∠3，∠1=∠2
∴∠2=∠3
又∵∠5=∠5
∴△ADF∽△FDG
∴
，
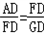设GD=x，则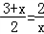
解得x1=1，x2=﹣4，经检验x1=1，x2=﹣4为所列方程的根
∵x2=﹣4＜0应舍去
∴GD=1由（1）已证EF∥BC
∴
．
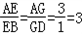∴∠4=∠2
又∵∠1=∠3，∠1=∠2
∴∠3=∠4
∴EF∥BC
（2）∵∠1=∠3，∠1=∠2
∴∠2=∠3
又∵∠5=∠5
∴△ADF∽△FDG
∴
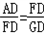，设GD=x，则
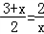
解得x1=1，x2=﹣4，经检验x1=1，x2=﹣4为所列方程的根
∵x2=﹣4＜0应舍去
∴GD=1由（1）已证EF∥BC
∴
．
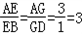练习册系列答案
名校课堂系列答案
相关题目
26、已知：如图，△ABC中，点D在AC的延长线上，CE是∠DCB的角平分线，且CE∥AB．
27、已知：如图，△ABC中，∠BAC=60°，D、E两点在直线BC上，连接AD、AE．
27、如图，△ABC中，AD⊥BC于D，DN⊥AC于N，DM⊥AB于M
14、如图，△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
已知，如图，△ABC中，点D在BC上，且∠1=∠C，∠2=2∠3，∠BAC=70°．