题目内容
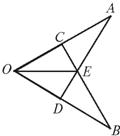 13、如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E,那么图中全等的三角形共有
13、如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E,那么图中全等的三角形共有4
对.分析:由于OA=OB,∠AOD=∠BOC,OC=OD,利用SAS可证△AOD≌△BOC,再利用全等三角形的性质,可知∠A=∠B;在△ACE和△BDE中,∠A=∠B,∠AEC=∠BED,而OA-OC=OB-OD,即AC=BD,利用AAS可证△ACE≌△BDE;再利用全等三角形的性质,可得AE=BE,在△AOE和△BOE中,由于OA=OB,∠A=∠B,AE=BE,利用SAS可证△AOE≌△BOE;再利用全等三角形的性质,可得∠COE=∠DOE,而OE=OE,OC=OD,利用SAS可证△COE≌△DOE.
解答: 解:∵OA=OB,∠AOD=∠BOC,OC=OD,
解:∵OA=OB,∠AOD=∠BOC,OC=OD,
∴△AOD≌△BOC,
∴∠A=∠B,
又∵∠AEC=∠BED,OA-OC=OB-OD,
即AC=BD,
∴△ACE≌△BDE,
∴AE=BE,
又∵OA=OB,∠A=∠B,
∴△AOE≌△BOE,
∴∠COE=∠DOE,
又∵OE=OE,OC=OD,
∴△COE≌△DOE.
故全等的三角形一共有4对.
故填4.
 解:∵OA=OB,∠AOD=∠BOC,OC=OD,
解:∵OA=OB,∠AOD=∠BOC,OC=OD,∴△AOD≌△BOC,
∴∠A=∠B,
又∵∠AEC=∠BED,OA-OC=OB-OD,
即AC=BD,
∴△ACE≌△BDE,
∴AE=BE,
又∵OA=OB,∠A=∠B,
∴△AOE≌△BOE,
∴∠COE=∠DOE,
又∵OE=OE,OC=OD,
∴△COE≌△DOE.
故全等的三角形一共有4对.
故填4.
点评:本题利用了全等三角形的判定和性质.做题时要从已知开始结合判定方法逐个验证,做到由易到难,不重不漏.

练习册系列答案
相关题目

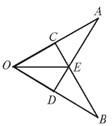 17、如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E,那么图中全等的三角形共有( )
17、如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E,那么图中全等的三角形共有( )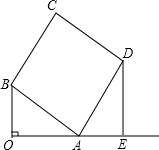 长线交于点E.
长线交于点E.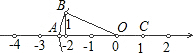 如图,已知OA=OB,那么数轴上点A与点C的距离是
如图,已知OA=OB,那么数轴上点A与点C的距离是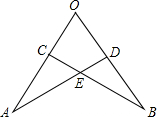 如图,已知OA=OB,OC=OD,下列结论中(1)∠A=∠B;(2)DE=CE;(3)连OE,OE平分∠O,正确的有
如图,已知OA=OB,OC=OD,下列结论中(1)∠A=∠B;(2)DE=CE;(3)连OE,OE平分∠O,正确的有