题目内容
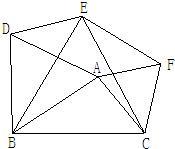 20、如图,分别以△ABC的三边为边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF.请回答下列问题:
20、如图,分别以△ABC的三边为边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF.请回答下列问题:(1)说明四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,四边形ADEF是菱形?
(4)当△ABC满足什么条件时,四边形ADEF是正方形?
(5)当△ABC满足什么条件时,以A,D,E,F为顶点的四边形不存在?
(第(2)(3)(4)(5)题不必说明理由)
分析:根据等边三角形的性质及平行四边形的判定(两组对边分别相等的四边形是平行边形)来证明四边形ADEF是平行四边形,同理可根据各多边形的判定方法来证明.
解答:解:(1)四边形ADEF是平行四边形.(1分)
∵等边三角形BCE和等边三角形ABD,
∴BE=BC,BD=BA.
又∵∠DBE=60°-∠ABE,∠ABC=60°-∠ABE,
∴∠DBE=∠ABC.
∴△BDE≌△BCA.(2分)
∴DE=AC.
∵在等边三角形ACF中,AC=AF,
∴DE=AF.
同理DA=EF.
∴四边形ADEF是平行四边形.(4分)
(2)当∠BAC=150°时,四边形ADEF是矩形.(5分)
(3)当AB=AC,或∠ABC=∠ACB=15°时,四边形ADEF是菱形.(6分)
(4)当∠BAC=150°且AB=AC,或∠ABC=∠ACB=15°时,四边形ADEF是正方形.(7分)
(5)当∠BAC=60°时,以A,D,E,F为顶点的四边形不存在.(8分)
∵等边三角形BCE和等边三角形ABD,
∴BE=BC,BD=BA.
又∵∠DBE=60°-∠ABE,∠ABC=60°-∠ABE,
∴∠DBE=∠ABC.
∴△BDE≌△BCA.(2分)
∴DE=AC.
∵在等边三角形ACF中,AC=AF,
∴DE=AF.
同理DA=EF.
∴四边形ADEF是平行四边形.(4分)
(2)当∠BAC=150°时,四边形ADEF是矩形.(5分)
(3)当AB=AC,或∠ABC=∠ACB=15°时,四边形ADEF是菱形.(6分)
(4)当∠BAC=150°且AB=AC,或∠ABC=∠ACB=15°时,四边形ADEF是正方形.(7分)
(5)当∠BAC=60°时,以A,D,E,F为顶点的四边形不存在.(8分)
点评:此题考查了学生对全等三角形,平行四边形,矩形,正方形,菱形的判定方法的理解及运用.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
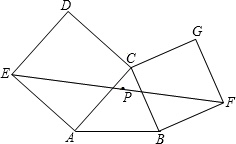 如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.
如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.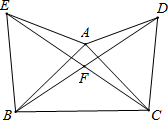 如图,分别以△ABC的边AB、AC向外作等边△ABE和等边△ACD,求证:BD=CE.
如图,分别以△ABC的边AB、AC向外作等边△ABE和等边△ACD,求证:BD=CE.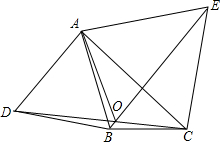 如图,分别以△ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断∠AOD与∠AOE的数量关系,并证明.
如图,分别以△ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断∠AOD与∠AOE的数量关系,并证明. 如图,分别以△ABC的边AB,AC向外作等边三角形ABD和等边三角形ACE,线段BE与CD相交于点O,连接OA.
如图,分别以△ABC的边AB,AC向外作等边三角形ABD和等边三角形ACE,线段BE与CD相交于点O,连接OA.