题目内容
某中学为了绿化校园,计划购买一批棕树和香樟树,经市场调查榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)请问榕树和香樟树的单价各多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵树不少于榕树的1.5倍,请你算算,该校本次购买榕树和香樟树共有哪几种方案.
(1)请问榕树和香樟树的单价各多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵树不少于榕树的1.5倍,请你算算,该校本次购买榕树和香樟树共有哪几种方案.
(1)榕树和香樟树的单价分别是60元/棵,80元/棵。
(2)有3种购买方案:
方案一:购买榕树58棵,香樟树92棵,
方案二:购买榕树59棵,香樟树91棵,
方案三:购买榕树60棵,香樟树90棵。
(2)有3种购买方案:
方案一:购买榕树58棵,香樟树92棵,
方案二:购买榕树59棵,香樟树91棵,
方案三:购买榕树60棵,香樟树90棵。
试题分析:(1)设榕树的单价为x元/棵,香樟树的单价是y元/棵,然后根据单价之间的关系和340元两个等量关系列出二元一次方程组,求解即可。
(2)设购买榕树a棵,表示出香樟树为(150﹣a)棵,然后根据总费用和两种树的棵数关系列出不等式组,求出a的取值范围,在根据a是正整数确定出购买方案。
解:(1)设榕树的单价为x元/棵,香樟树的单价是y元/棵,
根据题意得,
 ,解得
,解得 。
。答:榕树和香樟树的单价分别是60元/棵,80元/棵。
(2)设购买榕树a棵,则购买香樟树为(150﹣a)棵,
根据题意得,
 ,
,解不等式①得,a≥58,解不等式②得,a≤60,
∴不等式组的解集是58≤a≤60。
∵a只能取正整数,∴a=58、59、60。
∴有3种购买方案:
方案一:购买榕树58棵,香樟树92棵,
方案二:购买榕树59棵,香樟树91棵,
方案三:购买榕树60棵,香樟树90棵。

练习册系列答案
相关题目
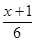 <
<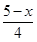 +1 (2)
+1 (2)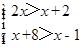
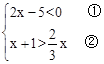 .
.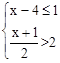 的解集是 .
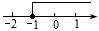
的解集是 .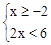 的解集在数轴上表示出来,正确的是
的解集在数轴上表示出来,正确的是



 ,且它的解是一对正数。
,且它的解是一对正数。 |。
|。 的解集在数轴上表示正确的是
的解集在数轴上表示正确的是