Question

某班要从演讲水平相当的甲、乙两人中选派一人参加学校的演讲大赛，为了公平，班委会设计了一个方法，其规则如下：在一个不透明的袋子里装有形状、大小、质地等完全相同的3个小球，把它们分别标上数字1、2、3，由甲从中随机摸出一个小球，记下小球上的数字；在另一个不透明口袋中装有形状、大小、质地等完全相同的4个小球，把它们分别标上数字1、2、3、4，由乙从口袋中随机摸出一个小球，记下小球上的数字，然后计算出这两个数字的和，若两个数字的和为奇数，则选甲去；若两个数字的和为偶数，则选乙去．
（1）请用树状图或列表的方法求甲被选去参加演讲大赛的概率；
（2）你认为这个方法公平吗？若公平，请说明理由；若不公平，请设计一个公平的方法．

Answer 1

解：（1）如图所示：

二次一次	1	2	3
1	2	3	4
2	3	4	5
3	4	5	6
4	5	6	7

则P（和为奇数）==；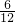

（2）答：公平．               理由如下：
∵P（和为偶数）==．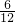
∵P（和为奇数）=P（和为偶数），
∴该方法公平．

分析：（1）列举出所有情况，再求出两个数字的和为奇数的概率即可；
（2）公平，因为两个概率相等．
点评：本题考查了随机事件的概率，解决本题的关键是得到相应的概率，概率相等就公平，否则就不公平．用到的知识点为：概率=所求情况数与总情况数之比．