Question

正方形的内切圆半径为r，这个正方形将它的外接圆分割出四个弓形，其中一个弓形的面积为

 

．

Answer 1

分析：先画出图形，根据垂径定理得出OE⊥BC，BE=

1

2

BC，再根据正方形的性质及勾股定理可表示出OB的长，
由S_弓形BFC=S_扇形BOC-S_△BOC即可解答．

解答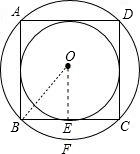：解：连接OE，OB，
∵OE=r，
∴BE=r，BC=2r，
即正方形的边长为2r，
由垂径定理得，OE⊥BC，BE=

1

2

BC，
∵四边形ABCD是正方形，
∴∠BOE=45°，
∴OE=BE=r，
由勾股定理得，OB²=OE²+BE²，
即OB²=r²+r²=2r²，OB=

2

r，
∴S_弓形BFC=S_扇形BOC-S_△BOC=

π( 2 r)2

4

-

1

2

×2r×r=

(π-2)r2

2

．

点评：本题考查的是正多边形和圆，熟知正方形的性质、勾股定理及垂径定理是解答此题的关键．