题目内容
正方形的内切圆半径为r,这个正方形将它的外接圆分割出四个弓形,其中一个弓形的面积为 .
【答案】分析:弓形的面积等于圆的面积减去正方形的面积再除以4即可求得,正方形的半径就是圆的半径,据此即可求得正方形的面积,从而求解.
解答:解:由已知得正方形的边长为2r,从而正方形的外接圆半径为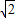 r,在圆的面积是:π(
r,在圆的面积是:π( r)2=2πr2,
r)2=2πr2,
正方形的面积是:4r2,
所求弓形的面积为 =(
=( π-1)r2.
π-1)r2.
故答案是:( π-1)r2.
π-1)r2.
点评:正多边形的计算基本思路是转化为解直角三角形.
解答:解:由已知得正方形的边长为2r,从而正方形的外接圆半径为
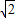 r,在圆的面积是:π(
r,在圆的面积是:π( r)2=2πr2,
r)2=2πr2,正方形的面积是:4r2,
所求弓形的面积为
 =(
=( π-1)r2.
π-1)r2.故答案是:(
 π-1)r2.
π-1)r2.点评:正多边形的计算基本思路是转化为解直角三角形.

练习册系列答案
相关题目