题目内容
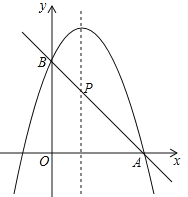
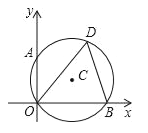
【题目】如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C上在第一象限内的一点且∠ODB=60°.
(1)求线段AB的长及⊙C的半径;
(2)求B点坐标.
【答案】(1)AB=4,⊙C的半径r=2;(2)(![]() ,0).
,0).
【解析】试题分析:(1)连接AB.由圆周角定理可知,AB必为⊙C的直径.Rt△ABO中,易知OA的长,而∠OAB=∠ODB=60°,通过解直角三角形,即可求得斜边AB的长,也就求得了⊙C的半径;
(2)在Rt△ABO中,由勾股定理即可求得OB的长,进而可得到B点的坐标.
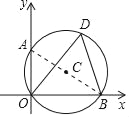
试题解析:解:(1)连接AB.∵∠ODB=∠OAB,∠ODB=60°,∴∠OAB=60°.
∵∠AOB是直角,∴AB是⊙C的直径,∠OBA=30°,∴AB=2OA=4,∴⊙C的半径r=2;
(2)在Rt△OAB中,由勾股定理得:OB2+OA2=AB2,∴OB=![]() ,∴B的坐标为:(
,∴B的坐标为:(![]() ,0).
,0).

练习册系列答案
相关题目
【题目】某地某月1~20日中午12时的气温(单位:℃)如下:
22 31 25 15 18 23 21 20 27 17 20 12 18 21 21 16 20 24 26 19
(1)将下列频数分布表补充完整:
气温分组 | 划记 | 频数 |
12≤x<17 |
| 3 |
17≤x<22 |
| 10 |
22≤x<27 |
| 5 |
27≤x<32 |
| 2 |

(2)补全频数分布直方图;
(3)根据频数分布表或频数分布直方图,分析数据的分布情况.