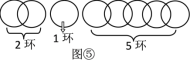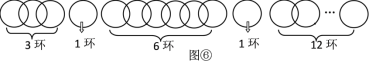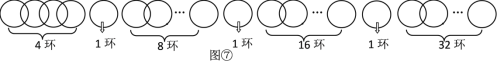题目内容
【题目】如图,正方形ABCD的边长为2,E、F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交AD于点M,交BA的延长线于点Q.连接BM,下列结论中:①AE=BF; ②AE⊥BF;③AQ=![]() ;④∠MBF=60°.
;④∠MBF=60°.
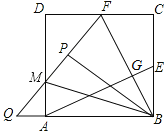
正确的结论是_____(填正确结论的序号).
【答案】①②③
【解析】
由题意可证△BFC≌△ABE,可判断①②,由折叠可判断④,根据勾股定理可求AM=![]() ,DM=
,DM=![]() ,根据平行线分线段成比例可求AQ=
,根据平行线分线段成比例可求AQ=![]() ,可判断③
,可判断③
∵四边形ABCD是正方形,
∴AB=BC=AD=CD=2,∠C=∠D=∠ABC=90°,
∵CF=BE,AB=BC,∠C=∠ABC,
∴△AEB≌△BCF,
∴AE=BF,∠EAB=∠FBC,
∵∠FBC+∠ABF=90°,
∴∠EAB+∠ABF=90°,
∴∠AGB=90°即AE⊥BF,
故①②正确,
∵折叠,
∴BC=BP,∠CBF=∠PBF,
∴AB=BP且BM=BM,
∴Rt△ABM≌Rt△BMP,
∴AM=MP,∠ABM=∠PBM,
∵∠ABM+∠PBM+∠CBF+∠PBF=90°,
∴∠MBF=45°,
故④错误,
∵在Rt△DMF中,MF2=FD2+DM2.
∴(1+AM)2=(2-AM)2+1,
∴AM=![]() ,
,
∴DM=![]() ,
,
∵CD∥BA,
∴![]() ,
,
∴AQ=![]()
故③正确
故答案是:①②③

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目