题目内容
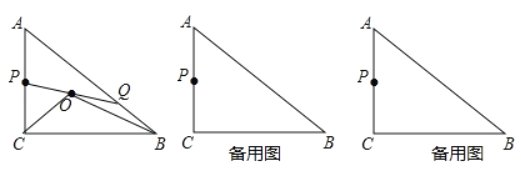
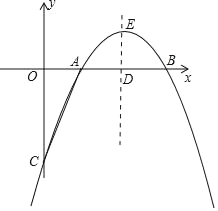
【题目】如图所示，已知抛物线y＝﹣x2+bx+c与x轴相交于A、B两点，且点A的坐标为（1，0），与y轴交于点C，对称轴直线x＝2与x轴相交于点D，点P是抛物线对称轴上的一个动点，以每秒1个单位长度的速度从抛物线的顶点E向下运动，设点P运动的时间为t（s）．
（1）点B的坐标为 ，抛物线的解析式是 ；
（2）求当t为何值时，△PAC的周长最小？
（3）当t为何值时，△PAC是以AC为腰的等腰三角形？
【答案】（1）（3，0），y＝﹣x2+4x﹣3；（2）t＝2；（3）t＝4或4+
或4﹣.
【解析】
（1）把A点坐标与对称轴x=1代入解析式即可求出b，c的值，即可求出解析式,故求出B点坐标；（2）由图可知，AC是定长，故只要求出PA+PC最小时，则△PAC的周长最小，又点A关于对称轴x=2的对称点是点B，故连接BC与抛物线对称轴的交点即为P点，此时PA+PC最小，则求出直线BC的解析式与x=2的交点即为P点坐标继而求出t的值；（3）根据AC为腰可分两种情况，①CP＝AC，可作图，根据AC＝CP＝
，CF＝2，利用勾股定理可求出PF的长，继而求出时间t，注意还要要分两种情况，②AC＝AP，可作图，利用Rt△OAC≌Rt△DAP，得出DP=CO=3，故而求出EP的长，即可求出时间t.
解：（1）根据题意得：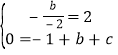
解得：b＝4，c＝﹣3
∴抛物线解析式y＝﹣x2+4x﹣3
当y＝0时，0＝﹣x2+4x﹣3
∴x1＝1，x2＝3
∴点B（3，0）
故答案为：（3，0），y＝﹣x2+4x﹣3
（2）如图：
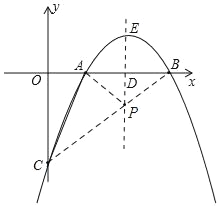
∵△PAC的周长＝AC+PA+PC
且AC是定长，
∴PA+PC最小时，△PAC的周长最小
∵点A，点B关于对称轴直线x＝2对称
∴连接BC交对称轴直线x＝2于点P
∵y＝﹣x2+4x﹣3与y轴交于点C，点E为抛物线的顶点
∴点C（0，﹣3），点E（2，1）
∴OC＝3，点D（2，0）即DE＝1
∵点B（3，0），点C（0，﹣3）
∴直线BC解析式：y＝x﹣3
当x＝2时，y＝﹣1
∴点P（2，﹣1）
∴t＝
＝2
（3）若CP＝AC时，如图：过点C作CF⊥ED于点F
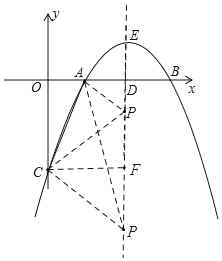
∵点A（1，0），点C（0，﹣3）
∴OA＝1，OC＝3
∵AC＝
＝
∵CF⊥DE，DE⊥OD，OC⊥OD
∴四边形ODFC是矩形
∴CF＝OD＝2，DF＝OC＝3
∵AC＝CP＝，CF＝2
∴PF＝
＝
∴DP＝3±
∴EP＝4±
∴t1＝
＝4+，t2＝
＝4﹣
若点AC＝AP时，如图
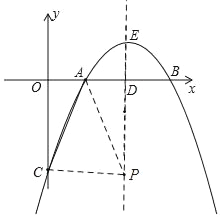
∵点A（1，0），点D（2，0）
∴OA＝AD＝1，且AC＝AP
∴Rt△OAC≌Rt△DAP（HL）
∴OC＝DP＝3
∴EP＝4
∴t＝
＝4
综上所述：t＝4或4+或4﹣.
