题目内容
【题目】将正整数1至2018按一定规律排列如下表:
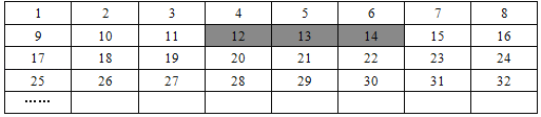
平移表中带阴影的方框,方框中三个数的和可能是_________.
【答案】3n(2≤n≤2015,且n为整数,且n≠8k+1,且n≠8k,1≤k≤252,且k为整数)
【解析】
设方框中三个数的中间数为n, 则另外两个数分别为n-1,n+1,根据题意可得出方框中三个数的中间数不能是每行的第一个数和第八个数,由此确定n的取值范围.
解:根据题意,需保证方框中的数在同一行,即方框中的中间的数不能是每行的第一个数和第八个数,如图,中间数为阴影部分的数,
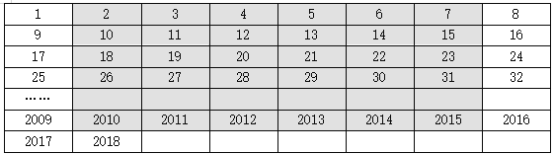
设中间数为n,(2≤n≤2015,且n为整数,且n≠8k+1,且n≠8k,1≤k≤252,且k为整数),则另外两个数分别为n-1,n+1,
n-1+n+n+1=3n
∴平移表中带阴影的方框,方框中三个数的和可能是3n(2≤n≤2015,且n为整数,且n≠8k+1,且n≠8k,1≤k≤252,且k为整数).
故答案为:3n(2≤n≤2015,且n为整数,且n≠8k+1,且n≠8k,1≤k≤252,且k为整数)

练习册系列答案
相关题目