��Ŀ����
����Ŀ��һ���ͳ��Ӽؿ����ҵأ�һ��������ҵؿ����أ�����ͬʱ��������ͳ���صľ���Ϊy1ǧ�ף������صľ���Ϊy2ǧ�ף�������ʻ��ʱ��ΪxСʱ��y1��y2����x�ĺ���ͼ����ͼ��ʾ�� 
��1������ͼ��ֱ��д��y1��y2����x�ĺ���ͼ���ϵʽ��
��2��������֮��ľ���ΪSǧ�ף���д��S����x�ĺ�����ϵʽ��
��3���ס������ؼ���A��B��������վ�����200ǧ�ף����ͳ�����A����վʱ�����ǡ�ý���B����վ����A����վ��صľ��룮
���𰸡�
��1���⣺��y1=k1x����ͼ��֪������ͼ���㣨10��600����
��10k1=600��
��ã�k1=60��
��y1=60x��0��x��10����
��y2=k2x+b����ͼ��֪������ͼ���㣨0��600������6��0������
![]() ��
��
��ã� ![]()
��y2=��100x+600��0��x��6��
��2���⣺�����⣬��
60x=��100x+600
x= ![]() ��
��
��0��x�� ![]() ʱ��S=y2��y1=��160x+600��
ʱ��S=y2��y1=��160x+600��
�� ![]() ��x��6ʱ��S=y1��y2=160x��600��
��x��6ʱ��S=y1��y2=160x��600��
��6��x��10ʱ��S=60x��
��S= 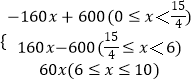
��3���⣺�����⣬��
�ٵ�A����վ�ڼ���B����վ֮��ʱ������100x+600����60x=200��
���x= ![]() ��
��
��ʱ��A����վ����أ�60�� ![]() =150km��
=150km��
�ڵ�B����վ�ڼ���A����վ֮��ʱ��60x������100x+600��=200��
���x=5����ʱ��A����վ����أ�60��5=300km��
����������A����վ���ؾ���Ϊ150km��300km
����������1��ֱ�����ô���ϵ�����Ϳ������y1��y2����x�ĺ���ͼ��ϵʽ����2���ֱ���ݵ�0��x�� ![]() ʱ����
ʱ���� ![]() ��x��6ʱ����6��x��10ʱ��������ɣ���3����A����վ�ڼ���B����վ֮�䣬B����վ�ڼ���A����վ֮����������г�������⼴�ɣ�
��x��6ʱ����6��x��10ʱ��������ɣ���3����A����վ�ڼ���B����վ֮�䣬B����վ�ڼ���A����վ֮����������г�������⼴�ɣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
