题目内容
（2012•南平模拟）如图：把一张给定大小的矩形卡片ABCD放在宽度为10mm的横格纸中，恰好四个顶点都在横格线上，已知α=25°，求长方形卡片的周长．（精确到1mm，参考数据：sin25°≈0.4，cos25°≈0.9，tan25°≈0.5）．分析：作AF⊥l4于F，交l2于E．在Rt△ABE中根据三角函数即可求得AB的长；在直角△AFD中，根据三角函数即可求得AD的长，从而求得长方形卡片的周长．
解答：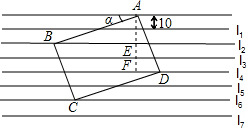
解：作AF⊥l4于F，交l2于E，则△ABE和△AFD均为直角三角形．
在Rt△ABE中，∠ABE=∠α=25°，
∴sin∠ABE=
，
∴AB=
=50．
∵∠FAD=90°-∠BAE，∠α=90°-∠BAE，
∴∠FAD=∠α=25°．
在Rt△AFD中，cos∠FAD=
，
∴AD=
≈44.4．
∴长方形卡片ABCD的周长为（44.4+50）×2≈189（mm）．
解：作AF⊥l4于F，交l2于E，则△ABE和△AFD均为直角三角形．在Rt△ABE中，∠ABE=∠α=25°，
∴sin∠ABE=
| AE |
| AB |
∴AB=
| 20 |
| 0.4 |
∵∠FAD=90°-∠BAE，∠α=90°-∠BAE，
∴∠FAD=∠α=25°．
在Rt△AFD中，cos∠FAD=
| AF |
| AD |
∴AD=
| 40 |
| 0.9 |
∴长方形卡片ABCD的周长为（44.4+50）×2≈189（mm）．
点评：本题考查了矩形对边相等的性质，直角三角形中三角函数的应用，锐角三角函数值的计算．通过作辅助线构造直角三角形是解决本题的关键．
练习册系列答案
相关题目
（2012•南平模拟）如图，有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等，把该套三角板放置在平面直角坐标系中，且
（2012•南平模拟）如图，已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C．