题目内容
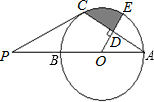 (2012•花都区一模)如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,连接AC,过点O作AC的垂线交AC于点D,交⊙O于点E.已知AB﹦8,∠P=30°.
(2012•花都区一模)如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,连接AC,过点O作AC的垂线交AC于点D,交⊙O于点E.已知AB﹦8,∠P=30°.(1)求线段PC的长;
(2)求阴影部分的面积.
分析:(1)连接OC,由PC为圆O的切线,根据切线的性质得到OC与PC垂直,可得三角形OCP为直角三角形,同时由直径AB的长求出半径OC的长,根据锐角三角函数定义得到tanP为∠P的对边OC与邻边PC的比值,根据∠P的度数,利用特殊角的三角函数值求出tanP的值,由tanP及OC的值,可得出PC的长;
(2)由直角三角形中∠P的度数,根据直角三角形的两个锐角互余求出∠AOC的度数,进而得出∠BOC的度数,由OD与BC垂直,且OC=OB,利用等腰三角形的三线合一得到OD为∠BOC的平分线,可求出∠COD度数为60°,再根据直角三角形中两锐角互余求出∠OCD度数为30°,根据30°角所对的直角边等于斜边的一半,由斜边OC的长求出OD的长,先由∠COD的度数及半径OC的长,利用扇形的面积公式求出扇形COE的面积,再由OD与CD的长,利用直角三角形两直角边乘积的一半求出直角三角形COD的面积,用扇形COE的面积减去三角形COD的面积,即可求出阴影部分的面积.
(2)由直角三角形中∠P的度数,根据直角三角形的两个锐角互余求出∠AOC的度数,进而得出∠BOC的度数,由OD与BC垂直,且OC=OB,利用等腰三角形的三线合一得到OD为∠BOC的平分线,可求出∠COD度数为60°,再根据直角三角形中两锐角互余求出∠OCD度数为30°,根据30°角所对的直角边等于斜边的一半,由斜边OC的长求出OD的长,先由∠COD的度数及半径OC的长,利用扇形的面积公式求出扇形COE的面积,再由OD与CD的长,利用直角三角形两直角边乘积的一半求出直角三角形COD的面积,用扇形COE的面积减去三角形COD的面积,即可求出阴影部分的面积.
解答: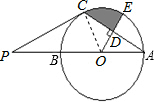 解:(1)连接OC,
解:(1)连接OC,
∵PC切⊙O于点C,
∴OC⊥PC,
∵AB=8,
∴OC=
AB=4,
又在直角三角形OCP中,∠P=30°,
∴tanP=tan30°=
,
即PC=
=4
;
(2)∵∠OCP=90°,∠P=30°,
∴∠COP=60°,
∴∠AOC=120°,
又AC⊥OE,OA=OC,
∴OD为∠AOC的平分线,
∴∠COE=
∠AOC=60°,又半径OC=4,
∴S扇形OCE=
=
,
在Rt△OCD中,∠COD=60°,
∴∠OCD=30°,
∴OD=
OC=2,
根据勾股定理得:CD=
=2
,
∴S△OCD=
DC•OD=
×2
×2=2
,
则S阴影=S扇形OCE-S△OCD=
-2
.
 解:(1)连接OC,
解:(1)连接OC,∵PC切⊙O于点C,
∴OC⊥PC,
∵AB=8,
∴OC=
| 1 |
| 2 |
又在直角三角形OCP中,∠P=30°,
∴tanP=tan30°=
| OC |
| PC |
即PC=
| 4 | ||||
|
| 3 |
(2)∵∠OCP=90°,∠P=30°,
∴∠COP=60°,
∴∠AOC=120°,
又AC⊥OE,OA=OC,
∴OD为∠AOC的平分线,
∴∠COE=
| 1 |
| 2 |
∴S扇形OCE=
| 60π×42 |
| 360 |
| 8π |
| 3 |
在Rt△OCD中,∠COD=60°,
∴∠OCD=30°,
∴OD=
| 1 |
| 2 |
根据勾股定理得:CD=
| OC2-OD2 |
| 3 |
∴S△OCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
则S阴影=S扇形OCE-S△OCD=
| 8π |
| 3 |
| 3 |
点评:此题考查了切线的性质,含30°角的直角三角形的性质,等腰三角形的性质,锐角三角函数定义,以及扇形的面积公式,遇到已知切线的类型题时,常常连接圆心与切点,利用切线的性质得出垂直,利用直角三角形的性质来解决问题.

练习册系列答案
相关题目
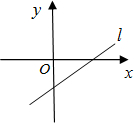 (2012•花都区一模)直线l:y=mx+n(m、n是常数)的图象如图所示,
(2012•花都区一模)直线l:y=mx+n(m、n是常数)的图象如图所示,