��Ŀ����
����Ŀ���Ķ�һ�����֣��ٻش��������⣺��֪��ƽ�������������Ϊ![]() ��
��![]() ������������빫ʽΪ
������������빫ʽΪ![]() ��ͬʱ����������ͬһ�������ϻ�����ֱ��ƽ����
��ͬʱ����������ͬһ�������ϻ�����ֱ��ƽ����![]() �ᡢƽ����
�ᡢƽ����![]() ��ʱ�������ľ��빫ʽ�ɻ����
��ʱ�������ľ��빫ʽ�ɻ����![]() ��
��![]() ��
��
��1������֪����![]() ��
��![]() ������
������![]() �����ľ��룻
�����ľ��룻
��2����֪��![]() ��ƽ����
��ƽ����![]() ���ֱ���ϣ���
���ֱ���ϣ���![]() ��������Ϊ7����
��������Ϊ7����![]() ��������Ϊ
��������Ϊ![]() ������
������![]() �����ľ��룻
�����ľ��룻
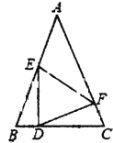
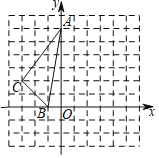
��3����֪һ�������θ����������Ϊ![]() ��
��![]() ��
��![]() �������ж��������Ƿ��ߣ���������˵�����ɣ��������������ͼ�ε������
�������ж��������Ƿ��ߣ���������˵�����ɣ��������������ͼ�ε������
���𰸡���1��![]() ����2��9����3��A��B��C���㲻���ߣ���ABC�����Ϊ
����2��9����3��A��B��C���㲻���ߣ���ABC�����Ϊ![]() ��
��
��������
��1�����������ľ��빫ʽ���м��㼴�ɣ�
��2�����ݵ�M��N��ƽ����y���ֱ���ϣ��������������ľ��빫ʽ![]() ���м��㣻
���м��㣻
��3�������A��B��C�����У���������֮��ľ��룬���жϳ����㲻���ߣ���һ�����ж�������ABC����״���Ӷ�������������
�⣺��1���ߵ�A��3��3����B��-2��-1����
��AB=![]() ��
��
��A��B�����ľ�����![]() ��
��
��2���ߵ�M��N��ƽ����y���ֱ���ϣ���M��������Ϊ7����N��������Ϊ-2��
��MN=|-2-7|=9��
��M��N�����ľ�����9��
��3�������㲻���ߣ���������Ϊֱ�������Σ��������£�
��һ�������θ����������Ϊ![]() ��
��
��AB=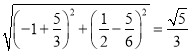 ��
��
AC=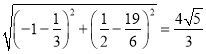 ��
��
BC=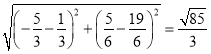 ��
��
��A��B��C���㲻���ߣ�
��AB2+AC2=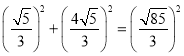 =BC2��
=BC2��
���ABC��ֱ�������Σ�
��S��ABC=![]() ABAC=
ABAC=![]() ��
��
��A��B��C���㲻���ߣ���ABC�����Ϊ![]() ��
��