题目内容
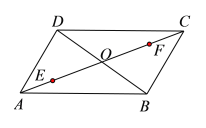
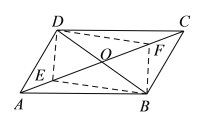
【题目】如图,已知平行四边形ABCD的对角线AC,BD相交于点O,AC=20 cm,BD=12 cm,两动点E,F同时以2 cm/s的速度分别从点A,C出发在线段AC上相对运动,点E到点C,点F到点A时停止运动.
(1)求证:当点E,F在运动过程中不与点O重合时,以点B,E,D,F为顶点的四边形为平行四边形;
(2)当点E,F的运动时间t为何值时,四边形BEDF为矩形?
【答案】(1)证明见解析(2)当点E,F的运动时间t为2 s或8 s时,四边形BEDF为矩形
【解析】
(1)如下图,连接DE,EB,BF,FD,由已知条件易得AE=CF,BO=DO,AO=CO,由此可得OE=OF,从而可得四边形BEDF是平行四边形;
(2)由(1)可知,四边形BEDF是平行四边形,故当EF=BD=12cm时,四边形BEDF是矩形,由此分以下两种情况进行解答即可求得对应的t的值,①点E在OA上,点F在OC上时,EF=BD=12cm;②点E在OC上,点F在OA上是,EF=BD=12cm.
(1)连接DE,EB,BF,FD.
∵两动点E,F同时以2 cm/s的速度分别从点A,C出发在线段AC上相对运动,
∴AE=CF.
∵平行四边形ABCD的对角线AC,BD相交于点O,
∴OD=OB,OA=OC(平行四边形的对角线互相平分),
∴OA-AE=OC-CF或AE-OA=CF-OC,即OE=OF,
∴四边形BEDF为平行四边形(对角线互相平分的四边形是平行四边形),
即以点B,E,D,F为顶点的四边形是平行四边形.
(2)由已知条件可得:AE=CF=2t,
∵由(1)可知四边形BEDF是平行四边形,
∴当EF=BD=12时,四边形BEDF是矩形.
①当点E在OA上,点F在OC上时,EF=AC-4t,
∵EF=BD=12,
∴20-4t=12,解得:t=2;
②当点E在OC上,点F在OA上时,EF=4t-AC=4t-20,
∵EF=BD=12,
∴4t-20=12,解得:t=8.
综上所述:当点E,F的运动时间t为2 s或8 s时,四边形BEDF为矩形.

 名校课堂系列答案
名校课堂系列答案【题目】列方程组解应用题某校组织“大手拉小手,义卖献爱心”活动,计划购买黑、白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花2400元购买了黑、白两种颜色的文化衫100件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑色文化衫 | 25 | 45 |
白色文化衫 | 20 | 35 |
(1)学校购进黑、白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.