题目内容
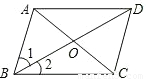
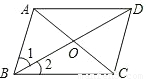
要使平行四边形ABCD为正方形,须再添加一定的条件,添加的条件可以是________.(填上一组符合题目要求的条件即可)
AC=BD且AC⊥BD或AB=BC且AB⊥BC等
分析:本题是开放题,可以针对正方形的判定方法,由给出条件四边形ABCD为平行四边形,加上条件AC=BD根据对角线相等的平行四边形为矩形,得到ABCD为矩形,再加上满足菱形的特点对角线AC与BD垂直,根据对角线垂直的矩形是正方形即可得证;或加上邻边AB与BC相等,根据邻边相等的平行四边形是菱形,得到ABCD为菱形,再加上AB垂直BC,即有一个角是直角的菱形为正方形,即可得证.答案可以有多种,主要条件明确,说法有理即可.
解答:本题答案不唯一,以下是其中两种解法:
(1)根据题意画出图形,如图所示:

添加的条件是AC=BD且AC⊥BD,此时平行四边形ABCD为正方形,
证明:∵四边形ABCD是平行四边形.又AC=BD,
∴四边形ABCD是矩形,
∵AC⊥BD,
∴四边形ABCD是正方形;
(2)添加的条件是AB=BC且AB⊥BC,此时平行四边形ABCD为正方形,
证明:∵四边形ABCD是平行四边形.又AB=BC,
∴四边形ABCD是菱形,
又∵AB⊥BC,即∠ABC=90°,
∴四边形ABCD是正方形.
故答案为:AC=BD且AC⊥BD或AB=BC且AB⊥BC等.
点评:此题主要考查矩形、菱形及正方形的判定,是一道开放型题.解答此类题的关键是要突破思维定势的障碍,运用发散思维,多方思考,探究问题在不同条件下的不同结论,挖掘它的内在联系,向“纵、横、深、广”拓展,从而寻找出添加的条件和所得的结论.
分析:本题是开放题,可以针对正方形的判定方法,由给出条件四边形ABCD为平行四边形,加上条件AC=BD根据对角线相等的平行四边形为矩形,得到ABCD为矩形,再加上满足菱形的特点对角线AC与BD垂直,根据对角线垂直的矩形是正方形即可得证;或加上邻边AB与BC相等,根据邻边相等的平行四边形是菱形,得到ABCD为菱形,再加上AB垂直BC,即有一个角是直角的菱形为正方形,即可得证.答案可以有多种,主要条件明确,说法有理即可.
解答:本题答案不唯一,以下是其中两种解法:
(1)根据题意画出图形,如图所示:

添加的条件是AC=BD且AC⊥BD,此时平行四边形ABCD为正方形,
证明:∵四边形ABCD是平行四边形.又AC=BD,
∴四边形ABCD是矩形,
∵AC⊥BD,
∴四边形ABCD是正方形;
(2)添加的条件是AB=BC且AB⊥BC,此时平行四边形ABCD为正方形,
证明:∵四边形ABCD是平行四边形.又AB=BC,
∴四边形ABCD是菱形,
又∵AB⊥BC,即∠ABC=90°,
∴四边形ABCD是正方形.
故答案为:AC=BD且AC⊥BD或AB=BC且AB⊥BC等.
点评:此题主要考查矩形、菱形及正方形的判定,是一道开放型题.解答此类题的关键是要突破思维定势的障碍,运用发散思维,多方思考,探究问题在不同条件下的不同结论,挖掘它的内在联系,向“纵、横、深、广”拓展,从而寻找出添加的条件和所得的结论.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
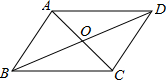 如图,要使平行四边形ABCD是矩形,则应添加的条件是
如图,要使平行四边形ABCD是矩形,则应添加的条件是