题目内容
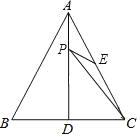
【题目】如图,在△ ABC 中,∠BAC=120°,AB=AC=4,AD⊥BC,延长AD至点E,使得AE=2AD,连接BE.

(1)求证:△ ABE 为等边三角形;
(2)将一块含 60°角的直角三角板 PMN 如图放置,其中点 P 与点 E 重合,且∠NEM=60°,边 NE 与 AB 交于点 G,边 ME 与 AC 交于点 F. 求证:BG=AF。
【答案】(1)见解析;(2)见解析
【解析】
(1)先证明∠ABD=90°-∠BAE=30°,可知AB=2AD,由因为AE=2AD,所以AB=AE,从而可知△ABE是等边三角形.
(2)由(1)可知:∠ABE=∠AEB=60°,AE=BE,然后求证△BEG≌△AEF即可得出BG=AF;
证明:(1)∵AB=AC,AD⊥BC,
![]()
∴ ∠ABD=90°-∠BAE=30°,∴ AB=2AD,
∵ AE=2AD,∴ AB=AE,
∵ ∠BAE=60°,∴△ABE 是等边三角形.
(2)∵ △ABE 是等边三角形,
∴ ∠ABE=∠AEB=60°,AE=BE①,
由(1)∠CAE=60°,∴ ∠ABE=∠CAE②,
∵ ∠NEM=∠BEA=60°,∴ ∠NEM-∠AEN=∠BEA-∠AEN,
∴ ∠AEF=∠BEG③,
由①②③得: △BEG≌△AEF(ASA)
∴ BG=AF.

 考前必练系列答案
考前必练系列答案【题目】甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图1所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.
(1)请填写下表:
平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
甲 | 80 | |||
乙 | 80 | 1060 |
(2)请回答下面问题
①从平均数和中位数来分析,甲,乙两城市的空气质量.
②从平均数和方差来分析,甲,乙两城市的空气质量情况.
③根据折线图上两城市的空气污染指数的走势及优的情况来分析两城市治理环境污染的效果.