题目内容
 如图,BE=CF,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且DB=DC.
如图,BE=CF,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且DB=DC.求证:(1)Rt△BED≌Rt△CFD;
(2)AD是∠BAC的平分线.
分析:(1)根据直角三角形全等的判定HL证出即可;
(2)由(1)推出DE=DF,根据角平分线性质推出即可.
(2)由(1)推出DE=DF,根据角平分线性质推出即可.
解答:证明:(1)∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
在Rt△BED和Rt△CFD中
,
∴Rt△BED≌Rt△CFD(HL).
证明:(2)∵Rt△BED≌Rt△CFD,
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD是∠BAC的平分线.
∴∠E=∠DFC=90°,
在Rt△BED和Rt△CFD中
|
∴Rt△BED≌Rt△CFD(HL).
证明:(2)∵Rt△BED≌Rt△CFD,
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD是∠BAC的平分线.
点评:本题考查了全等三角形的性质和判定和角平分线性质的应用,关键是运用定理进行推理,题目比较典型,难度适中.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
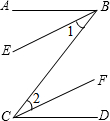 完成推理过程并填写推理理由:
完成推理过程并填写推理理由: 已知:如图,BE∥CF,BE上的一点A满足AE=CF,AD∥BC,E,D,F三点在一条直线上,EF与BC交于G点.
已知:如图,BE∥CF,BE上的一点A满足AE=CF,AD∥BC,E,D,F三点在一条直线上,EF与BC交于G点. 如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,
如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC, 如图,BE=CF,AB=DE,添加下列哪些条件可以推证△ABC≌△DFE( )
如图,BE=CF,AB=DE,添加下列哪些条件可以推证△ABC≌△DFE( )