Question

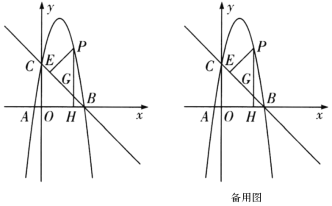
【题目】如图，在矩形中，，，连接，并过点作，垂足为，直线垂直，分别交、于点、．直线从出发，以每秒的速度沿方向匀速运动到为止；点沿线段以每秒的速度由点向点匀速运动，到点为止，直线与点同时出发，设运动时间为秒（）．

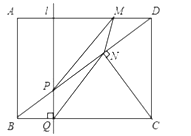
（1）线段_________；

（2）连接和，当四边形为平行四边形时，求的值；

（3）在整个运动过程中，当为何值时的面积取得最大值，最大值是多少？

Answer 1

【答案】（1）；（2）；（3）时，的面积取得最大值，最大值为．

【解析】

（1）由矩形的性质和勾股定理可求BD的长，由三角形的面积公式可求CN的长；

（2）由勾股定理可求DN的长，通过证明△DMN∽△DAB，可得，可得DM的值，即可求t的值；

（3）分两种情况讨论，利用三角形面积公式列出△PMN的面积与t的关系式，可求△PMN的面积的最大值．

（1）∵四边形是矩形

∴，，

∴，

∵

∴

故答案为：;

（2）在中，

∵四边形为平行四边形时

∴，且，

∴

∴

∴

∴

即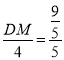

∴

∴;

（3）∵，∴

如图，过点作于点，

∵

∴

∴

当

∵，

∴，

∴

∴=

∴当时，有最大值，且最大值为，

则当时，点与点重合时，点，点，点不构成三角形；

当时，如图，

∴

∴=

当时，随的增大而增大，

∴当时，最大值为，

∵

∴综上所述：时，的面积取得最大值，最大值为．