Question

（2012•乌鲁木齐）如图是一个抛物线形拱桥的示意图，桥的跨度AB为100米，支撑桥的是一些等距的立柱，相邻立柱的水平距离为10米（不考虑立柱的粗细），其中距A点10米处的立柱FE的高度为3.6米．
（1）求正中间的立柱OC的高度；
（2）是否存在一根立柱，其高度恰好是OC的一半？请说明理由．

Answer 1

分析：（1）如图，以点O为原点，以AB所在的直线为x轴，建立直角坐标系．问题转化为求点C的纵坐标，该抛物线对应的函数关系式为：y=ax²+c，根据题意知道其上两点，求出a，c；
（2）设存在一根系杆的长度恰好是OC长度的一半，即为5米，解得x，然后再作讨论．

解答：解：（1）根据题意可得中间立柱OC经过AB的中点O．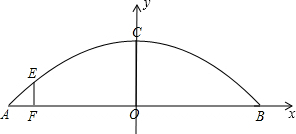
如图，以点O为原点，以AB所在的直线为x轴，建立直角坐标系．
问题转化为求点C的纵坐标．
|OF|=40（米），故B（50，0），E（-40，3.6）
设抛物线的解析式为y=ax²+c
∴

502a+c=0 402a+c=3.6

解得：

a=- 1 250 c=10

∴y=-

1

250

x²+10，当x=0时，y=10
即正中间的立柱OC的高度是10（米）；

（2）设存在一根立柱的高度是OC的一半，即这根立术的高度是5米．
则有5=-

1

250

x²+10．解得：x=±25

2

∵相邻立柱之间的间距为10米．最中间的立柱OC在y轴上，
根据题意每根立柱上的点的横坐标为10的整数倍，
∴x=±25

2

与题意不符，
∴不存在一根立柱，其高度恰好是OC高度的一半．

点评：此题主要考查了二次函数的应用，运用二次函数解决实际问题建立坐标系得出点的坐标是解题关键．