��Ŀ����
����Ŀ��ij��ҵ������һ����Ʒ���к�30����ȫ�����꣬���鷢�֣������г�����������Ϊy1���֣���ʱ��t��tΪ��������λ���죩�Ĺ�ϵ��ͼ1��ʾ�������ߵ�һ���֣��������г�����������y2���֣���ʱ��t��tΪ��������λ���죩�Ĺ�ϵ��ͼ2��ʾ��
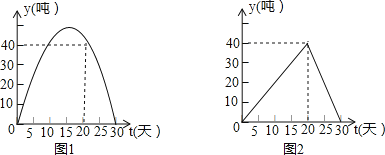
��1����y1��ʱ��t�ĺ�����ϵʽ���Ա���t��ȡֵ��Χ����д��y2��t�ĺ�����ϵʽ���Ա���t��ȡֵ��Χ��
��2������ڡ������г�������������Ϊy�֣�ֱ��д��y��ʱ��t�ĺ�����ϵʽ�������۵ڼ���ʱ�����ڡ����г�����������������ﵽ75�֣�
��3���ж����еڼ�����ڡ������г�������������y��������ʱ�����ֵ��
���𰸡�(1)��y1=-![]() t2+6t����0��t��30����tΪ������y2=
t2+6t����0��t��30����t������y2=![]() �� t����
�� t����
(2)��15�죻
(3)�����е�20����ڡ������г�������������y���Ϊ80��.
��������
���������(1)����������κ����Ľ���ʽΪy1=at2+bt��Ȼ��������������������ʽ������ͼ��ó��Ա�����ȡֵ��Χ��һ�κ���Ϊ�ֶκ�������0��t��20ʱΪ��������������20��t��30ʱΪһ�κ�����(2)������y=y1+y2�г���������ʽ��Ȼ�����t��ֵ��(3)�����ݷֶκ����ֱ����ÿһ�����������ֵ��Ȼ��ó����.
���������(1)���躯����ϵʽy1=at2+bt��
������ã�![]() �� ���
�� ���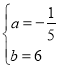 �� ��y1=-
�� ��y1=-![]() t2+6t����0��t��30����t����
t2+6t����0��t��30����t����
��y2=kt+b�� ��0��t��20ʱ��y2=2t��
��20��t��30ʱ��![]() �� ���
�� ���![]() ��
��
��y2=![]() �� t����
�� t����
(2)����y=y1+y2��֪�� y=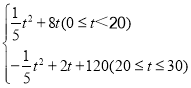
��ͼ���֪������20�죬y=80�� ��y=75ʱ��t��20�� ��-![]() t2+8t=75��
t2+8t=75��
��ã�t1=15��t2=25����ȥ��
�����۵�15��ʱ�����ڡ����г�����������������ﵽ75�֣�
(3)����0��t��20ʱ��y=-![]() t2+8t=-
t2+8t=-![]() ��t-20��2+80��
��t-20��2+80��
��tΪ������ ����t=19ʱ��y���ֵΪ79��8�֣�
��20��t��30ʱ��y=-![]() t2+2t+120=-
t2+2t+120=-![]() ��t-5��2+125��
��t-5��2+125��
��y��x�������С�� ����t=20ʱ��y���ֵΪ80�֣�
���е�20����ڡ������г�������������y���Ϊ80�֣�