题目内容
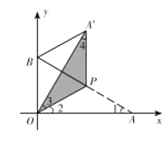
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,
放置在平面直角坐标系中,![]() 是坐标原点,点
是坐标原点,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点(点
上一点(点![]() 不与点
不与点![]() ,点
,点![]() 重合),沿
重合),沿![]() 折叠该纸片,点
折叠该纸片,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() .
.

(1)如图1,当点![]() 在第一象限,且
在第一象限,且![]() 时,求点
时,求点![]() 的坐标;
的坐标;
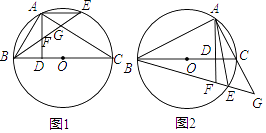
(2)如图2,当点![]() 为
为![]() 的中点时;
的中点时;
①求证:![]() ;
;
②直接写出四边形![]() 的面积;
的面积;
(3)当![]() 时,直接写出点
时,直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)①见解析;②
;(2)①见解析;②![]() ;(3)点
;(3)点![]() 的坐标(
的坐标(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由点A和B的坐标得出OA=![]() ,OB=2,由折叠的性质得:OA'=OA=
,OB=2,由折叠的性质得:OA'=OA=![]() ,由勾股定理求出A'B=
,由勾股定理求出A'B=![]() ,即可得出点A'的坐标为(
,即可得出点A'的坐标为(![]() ,2);
,2);
(2)①由直角三角形斜边上的中线得∠1=∠2=30゜,由折叠得∠3=∠4=30゜,故可得![]() ,从而可得结论;
,从而可得结论;
②由折叠得![]() ,根据直角三角形中30゜角对的直角边等于斜边的一半得
,根据直角三角形中30゜角对的直角边等于斜边的一半得![]() ,进一步可求出四边形
,进一步可求出四边形![]() 的面积;
的面积;
(3)分两种情况:①易得∠APA'=150°,连接AA′,延长OP交AA′于E,则∠APE=75°,∠OPB=75°,求出AB=![]() ,则∠BAO=30°,∠OBA=60°,推出∠BA′P=30°,∠OPA′=105°,得出∠A′OP=45°,则点A'在y轴上,∠A'OP=∠AOP=
,则∠BAO=30°,∠OBA=60°,推出∠BA′P=30°,∠OPA′=105°,得出∠A′OP=45°,则点A'在y轴上,∠A'OP=∠AOP=![]() ∠AOB=45°,得出点P在∠AOB的平分线上,由待定系数法求出直线AB的解析式为y=-
∠AOB=45°,得出点P在∠AOB的平分线上,由待定系数法求出直线AB的解析式为y=-![]() x+2,即可得出点P的坐标;
x+2,即可得出点P的坐标;
②由折叠的性质得:∠A'=∠A=30°,OA'=OA,作出四边形OAPA'是菱形,得出PA=OA=![]() ,作PM⊥OA于M,由直角三角形的性质求出PM=
,作PM⊥OA于M,由直角三角形的性质求出PM=![]() PA=
PA=![]() ,把y=
,把y=![]() 代入y=-
代入y=-![]() x+1求出点P的纵坐标即可.
x+1求出点P的纵坐标即可.
(1)解: ∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() 折叠得到
折叠得到![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.
(2)①证明:如图,在![]() 中,
中,![]() ,
,
![]() 为
为![]() 的中点,即
的中点,即![]() 为中线,
为中线,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() 折叠得到
折叠得到![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
②过![]() 点作
点作![]() 轴,
轴,
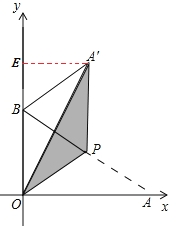
在Rt△ABO中,OA=![]() ,OB=2,
,OB=2,
∴AB=![]() ,
,
∵P是AB的中点,
∴AP=BP=2,OP=![]() AB=2,
AB=2,
∴OB=OP=BP
∴![]()
∴![]() ,
,
∵OB∥PA',
∴四边形OPA'B是平行四边形,
由①得,![]()
∴![]()
∴四边形OPA'B的面积为![]() ;
;
(3)设P(x,y),分两种情况:
①∵∠BPA'=30°,
∴∠APA'=150°,
连接AA′,延长OP交AA′于E,如图③所示:
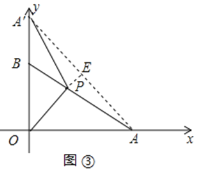
则∠APE=75°,
∴∠OPB=75°,
∵OA=![]() ,OB=1,
,OB=1,
∴AB=![]() =4,
=4,
∵∠OBA=60°,
∴![]()
∴![]()
∵∠BPA'=30°,
∴∠OPA′=105°,
∴∠A′OP=180°-30°-105°=45°,
∴点A'在y轴上,
∴∠A'OP=∠AOP=![]() ∠AOB=45°,
∠AOB=45°,
∴点P在∠AOB的平分线上,
设直线AB的解析式为y=kx+b,
把点A(![]() ,0),点B(0,1)代入得:
,0),点B(0,1)代入得:
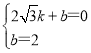 ,
,
解得: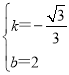 ,
,
∴直线AB的解析式为y=-![]() x+2,
x+2,
∵点P在∠AOB的一部分线上
∴P(x,x),
∴x=-![]() x+2,
x+2,
解得:x=![]() ,
,
∴P(![]() ,
,![]() );
);
②如图④所示:
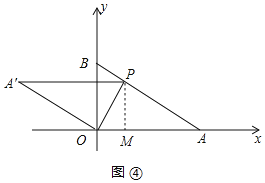
由折叠的性质得:∠A'=∠A=30°,OA'=OA,
∵∠BPA'=30°,
∴∠A'=∠A=∠BPA',
∴OA'∥AP,PA'∥OA,
∴四边形OAPA'是菱形,
∴PA=OA=![]() ,
,
作PM⊥OA于M,如图④所示:
∵∠A=30°,
∴PM=![]() PA=
PA=![]() ,
,
把y=![]() 代入y=-
代入y=-![]() x+2得:
x+2得:![]() =-
=-![]() x+2,
x+2,
解得:x=![]() ,
,
∴P(![]() ,
,![]() );
);
综上所述:当∠BPA'=30°时,点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案