题目内容
【题目】抛物线y=4x2﹣2ax+b与x轴相交于A（x1 ， 0），B（x2 ， 0）（0＜x1＜x2）两点，与y轴交于点C．
（1）设AB=2，tan∠ABC=4，求该抛物线的解析式；
（2）在（1）中，若点D为直线BC下方抛物线上一动点，当△BCD的面积最大时，求点D的坐标；
（3）是否存在整数a，b使得1＜x1＜2和1＜x2＜2同时成立，请证明你的结论．
【答案】
（1）
解：∵tan∠ABC=4
∴可以假设B（m，0），则A（m﹣2，0），C（0，4m），
∴可以假设抛物线的解析式为y=4（x﹣m）（x﹣m+2），
把C（0，4m）代入y=4（x﹣m）（x﹣m+2），得m=3，
∴抛物线的解析式为y=4（x﹣3）（x﹣1），
∴y=4x2﹣16x+12
（2）
解：如图，设P（m，4m2﹣16m+12）．作PH∥OC交BC于H．
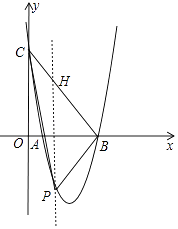
∵B（3，0），C（0，12），
∴直线BC的解析式为y=﹣4x+12，
∴H（m，﹣4m+12），
∴S△PBC=S△PHC+S△PHB= 
（﹣4m+12﹣4m2+16m﹣12）3=﹣6（m﹣ 
）2+ 
，
∵﹣6＜0，
∴m= 时，△PBC面积最大，
此时P（ ，﹣3）
（3）
解：不存在．
理由：假设存在．由题意可知，
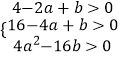且1＜﹣ 
＜2，
∴4＜a＜8，
∵a是整数，
∴a=5 或6或7，
当a=5时，代入不等式组，不等式组无解．
当a=6时，代入不等式组，不等式组无解．
当a=7时，代入不等式组，不等式组无解．
综上所述，不存在整数a、b，使得1＜x1＜2和1＜x2＜2同时成立
【解析】（1）由tan∠ABC=4，可以假设B（m，0），则A（m﹣2，0），C（0，4m），可得抛物线的解析式为y=4（x﹣m）（x﹣m+2），把C（0，4m）代入y=4（x﹣m）（x﹣m+2），求出m的值即可解决问题；（2）设P（m，4m2﹣16m+12）．作PH∥OC交BC于H，根据S△PBC=S△PHC+S△PHB构建二次函数，理由二次函数的性质解决问题；（3）不存在．假设存在，由题意由题意可知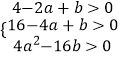， 且1＜﹣ ＜2，首先求出整数a的值，代入不等式组，解不等式组即可解决问题．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．
