题目内容
【题目】已知关于x的一元二次方程x2﹣8x﹣k2＝0（k为常数）．
（1）求证：方程有两个不相等的实数根；
（2）设x1，x2为方程的两个实数根，且x1+2x2＝7，试求出方程的两个实数根和k的值．
【答案】（1）详见解析；（2）k＝±3，方程的两个根分别为9和－1．
【解析】
（1）要证明方程有两个不相等的实数根，只要证明判别式△＝b2﹣4ac的值大于0即可；
（2）根据一元二次方程的根与系数的关系可以得到两根的和是8，结合x1+2x2＝7即可求得方程的两个实根，进而可求k的值．
（1）∵b2﹣4ac＝（﹣8）2﹣4×1×（﹣k2）＝64+4k2＞0，∴方程有两个不相等的实数根；
（2）∵x1+x2＝8．
又∵x1+2x2＝7，解得：
，将x2＝﹣1代入原方程得：（﹣1）2﹣8×（﹣1）﹣k2＝0，解得：k＝±3．
【题目】主题班会上，王老师出示了如图所示的一幅漫画，经过同学们的一番热议，达成以下四个观点：
A．放下自我，彼此尊重； B．放下利益，彼此平衡；
C．放下性格，彼此成就； D．合理竞争，合作双赢．
要求每人选取其中一个观点写出自己的感悟．根据同学们的选择情况，小明绘制了下面两幅不完整的图表，请根据图表中提供的信息，解答下列问题：
观点 | 频数 | 频率 |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |
（1）参加本次讨论的学生共有 人；表中a＝ ，b＝ ；
（2）在扇形统计图中，求D所在扇形的圆心角的度数；
（3）现准备从A，B，C，D四个观点中任选两个作为演讲主题，请用列表或画树状图的方法求选中观点D（合理竞争，合作双赢）的概率．
【题目】一粒木质中国象棋棋子“車”，它的正面雕刻一个“車”字，它的反面是平的，将棋子从一定高度下抛，落地反弹后可能是“車”字面朝上，也可能是“車”字朝下．由于棋子的两面不均匀，为了估计“車”字朝上的机会，某实验小组做了棋子下抛实验，并把实验数据整理如下：
实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“車”字朝上的频数 | 14 | 18 | 38 | 47 | 52 |
| 78 | 88 |
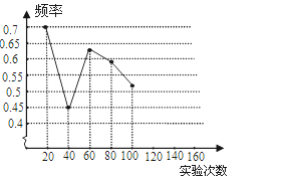
相应的频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.55 | 0.56 |
|
（1）请将表中数据补充完整，并画出折线统计图中剩余部分．
（2）如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的机会，请估计这个机会约是多少？
（3）在（2）的基础上，进一步估计：将该“車”字棋子，按照实验要求连续抛2次，则刚好使“車”字一次字面朝上，一次朝下的可能性为多少？
