题目内容
【题目】如图1，在直角坐标系中，O是坐标原点，点A在y轴正半轴上，二次函数y=ax2+ 
x+c的图象F交x轴于B、C两点，交y轴于M点，其中B（﹣3，0），M（0，﹣1）．已知AM=BC．
（1）求二次函数的解析式；
（2）证明：在抛物线F上存在点D，使A、B、C、D四点连接而成的四边形恰好是平行四边形，并请求出直线BD的解析式；
（3）在（2）的条件下，设直线l过D且分别交直线BA、BC于不同的P、Q两点，AC、BD相交于N．
①若直线l⊥BD，如图1，试求 
的值；
②若l为满足条件的任意直线．如图2．①中的结论还成立吗？若成立，证明你的猜想；若不成立，请举出反例．
【答案】
（1）
解：∵二次函数y=ax2+ 
x+c的图象经过点B（﹣3，0），M（0，﹣1），
∴ 
，
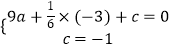解得a= ，c=﹣1．
∴二次函数的解析式为：y= x2+ x﹣1
（2）
解：由二次函数的解析式为：y= x2+ x﹣1，
令y=0，得 x2+ x﹣1=0，
解得x1=﹣3，x2=2，∴C（2，0），∴BC=5；
令x=0，得y=﹣1，∴M（0，﹣1），OM=1．
又AM=BC，∴OA=AM﹣OM=4，∴A（0，4）．
设AD∥x轴，交抛物线于点D，如图1所示，
则yD= x2+ x﹣1=OA=4，
解得x1=5，x2=﹣6（位于第二象限，舍去）
∴D点坐标为（5，4）．
∴AD=BC=5，
又∵AD∥BC，
∴四边形ABCD为平行四边形．
即在抛物线F上存在点D，使A、B、C、D四点连接而成的四边形恰好是平行四边形．
设直线BD解析式为：y=kx+b，∵B（﹣3，0），D（5，4），
∴ 
，
解得：k= 
，b= 
，
∴直线BD解析式为：y= x+
（3）
解：在Rt△AOB中，AB= 
=5，又AD=BC=5，∴ABCD是菱形．
①若直线l⊥BD，如图1所示．
∵四边形ABCD是菱形，
∴AC⊥BD，
∴AC∥直线l，
∴ 
，
∵BA=BC=5，
∴BP=BQ=10，
∴ 
= 
= 
；
②若l为满足条件的任意直线，如图2所示，此时①中的结论依然成立，理由如下：
∵AD∥BC，CD∥AB，
∴△PAD∽△DCQ，
∴ 
，∴APCQ=ADCD=5×5=25．
∴
= 
= 
= 
= 
= 
= ．
【解析】（1）利用待定系数法求出二次函数的解析式；（2）首先求出D点的坐标，可得AD=BC且AD∥BC，所以四边形ABCD是平行四边形；再根据B、D点的坐标，利用待定系数法求出直线BD的解析式；（3）本问的关键是判定平行四边形ABCD是菱形．①推出AC∥直线l，从而根据平行线间的比例线段关系，求出BP、CQ的长度，计算出 = ；②判定△PAD∽△DCQ，得到APCQ=25，利用这个关系式对 进行分式的化简求值，结论为 = 不变．
【考点精析】通过灵活运用平行四边形的判定与性质，掌握若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积即可以解答此题．
