题目内容
已知x1,x2是关于x的方程(x-2)(x-m)=(p-2)(p-m)的两个实数根.(1)求x1,x2的值;
(2)若x1,x2是某直角三角形的两直角边的长,问当实数m,p满足什么条件时,此直角三角形的面积最大?并求出其最大值.
【答案】分析:(1)化简方程,用分解因式法求出两根;
(2)直角三角形的面积为 x1x2,利用根与系数的关系可以得到关于p的关系式,然后利用二次函数可以求出什么时候有最大值.
x1x2,利用根与系数的关系可以得到关于p的关系式,然后利用二次函数可以求出什么时候有最大值.
解答:解:(1)原方程变为:x2-(m+2)x+2m=p2-(m+2)p+2m,
∴x2-p2-(m+2)x+(m+2)p=0,
(x-p)(x+p)-(m+2)(x-p)=0,
即(x-p)(x+p-m-2)=0,
∴x1=p,x2=m+2-p;
(2)根据(1)得到
直角三角形的面积为 x1x2=
x1x2= p(m+2-p)
p(m+2-p)
=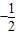 p2+
p2+ (m+2)p
(m+2)p
=- (p-
(p-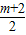 )2+
)2+ ,
,
∴当p= (m>-2)时,以x1,x2为两直角边长的直角三角形的面积最大,最大面积为
(m>-2)时,以x1,x2为两直角边长的直角三角形的面积最大,最大面积为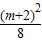 .
.
点评:本题是综合性较强的题,利用了分解因式法求方程的根,利用了二次函数求最值.
(2)直角三角形的面积为
 x1x2,利用根与系数的关系可以得到关于p的关系式,然后利用二次函数可以求出什么时候有最大值.
x1x2,利用根与系数的关系可以得到关于p的关系式,然后利用二次函数可以求出什么时候有最大值.解答:解:(1)原方程变为:x2-(m+2)x+2m=p2-(m+2)p+2m,
∴x2-p2-(m+2)x+(m+2)p=0,
(x-p)(x+p)-(m+2)(x-p)=0,
即(x-p)(x+p-m-2)=0,
∴x1=p,x2=m+2-p;
(2)根据(1)得到
直角三角形的面积为
 x1x2=
x1x2= p(m+2-p)
p(m+2-p)=
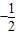 p2+
p2+ (m+2)p
(m+2)p=-
 (p-
(p-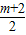 )2+
)2+ ,
,∴当p=
 (m>-2)时,以x1,x2为两直角边长的直角三角形的面积最大,最大面积为
(m>-2)时,以x1,x2为两直角边长的直角三角形的面积最大,最大面积为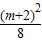 .
.点评:本题是综合性较强的题,利用了分解因式法求方程的根,利用了二次函数求最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目