题目内容
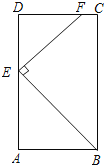
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为边
为边![]() 上一动点,点
上一动点,点![]() 为射线
为射线![]() 上一动点,且
上一动点,且![]() .
.
(1)当![]() 时,联结
时,联结![]() ,求
,求![]() 的余切值;
的余切值;
(2)当点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)联结![]() ,若
,若![]() 为等腰三角形,求
为等腰三角形,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 为6或7.
为6或7.
【解析】
(1)先根据勾股定理求出AB的长度,再由三角形的中位线定理求出DF、DE的长,由锐角三角函数的定义即可求出![]() 的余切值;
的余切值;
(2)过点E作EH⊥AC于点H,由平行线的性质及等腰三角形的性质可求出HE、HD的表达式,再由相似三角形的判定定理求出![]() ,根据相似三角形的性质即可写出y关于x的函数解析式;
,根据相似三角形的性质即可写出y关于x的函数解析式;
(3)先分析出![]() 为等腰三角形时的两种情况,再根据题意画出图形,当DC=DE时,点F在边BC上,过点
为等腰三角形时的两种情况,再根据题意画出图形,当DC=DE时,点F在边BC上,过点![]() 作
作![]() 于点
于点![]() 可求出AE的长度,由AE的长可判断出点F的位置,进而求出BF的长;当ED=EC时,先判断出点F的位置,再根据相似三角形的性质及判定定理即可解答.
可求出AE的长度,由AE的长可判断出点F的位置,进而求出BF的长;当ED=EC时,先判断出点F的位置,再根据相似三角形的性质及判定定理即可解答.
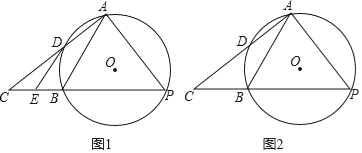
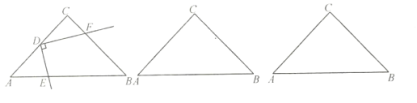
解:(1)如图1所示,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
在![]() 中,
中,![]()
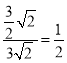 .
.
(2)过点![]() 作
作![]() 于点
于点![]() (图2),设AE=x,
(图2),设AE=x,
∵BC⊥AC,
∴EH∥BC,
∴∠AEH=∠B,
∵∠B=∠A,
∴∠AEH=∠A,![]() ,
,
![]() ,
,
又可证![]() ,
,
![]() ,
,
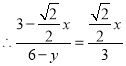 ,
,
![]() ;
;

(3)![]() ,
,![]() ,
,
![]() ,
,
![]() 若
若![]() 为等腰三角形,只有
为等腰三角形,只有![]() 或
或![]() 两种可能.
两种可能.
①当![]() 时,点
时,点![]() 在边
在边![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() (如图①),可得:
(如图①),可得:![]() ,即点
,即点![]() 在
在![]() 中点,
中点,
![]() 此时
此时![]() 与
与![]() 重合,
重合,![]() ;
;
②当![]() 时,点
时,点![]() 在
在![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 于点
于点![]() (如图②),
(如图②),
∴![]() ,
,
![]() ,
,
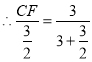 ,
,
![]() ,
,
![]() ,
,
综上所述,![]() 为6或7.
为6或7.

 应用题天天练四川大学出版社系列答案
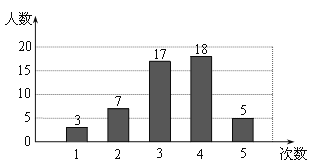
应用题天天练四川大学出版社系列答案【题目】小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)实验.
![]() 他们在一次实验中共掷骰子
他们在一次实验中共掷骰子![]() 次,试验的结果如下:
次,试验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
①填空:此次实验中“![]() 点朝上”的频率为________;
点朝上”的频率为________;
②小红说:“根据实验,出现![]() 点朝上的概率最大.”她的说法正确吗?为什么?
点朝上的概率最大.”她的说法正确吗?为什么?
![]() 小颖和小红在实验中如果各掷一枚骰子,那么枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
小颖和小红在实验中如果各掷一枚骰子,那么枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
【题目】某公司经销一种成本为10元的产品,经市场调查发现,在一段时间内,销售量![]() (件)与销售单价
(件)与销售单价![]() ( 元/件 )的关系如下表:
( 元/件 )的关系如下表:
|
| 15 | 20 | 25 | 30 |
|
|
| 550 | 500 | 450 | 400 |
|
设这种产品在这段时间内的销售利润为![]() (元),解答下列问题:
(元),解答下列问题:
(1)如![]() 是
是![]() 的一次函数,求
的一次函数,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)求销售利润![]() 与销售单价
与销售单价![]() 之间的函数关系式;
之间的函数关系式;
(3)求当![]() 为何值时,
为何值时,![]() 的值最大?最大是多少?
的值最大?最大是多少?