题目内容
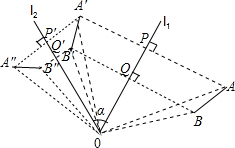
 设直线l1和直线l2相交,交点为O,其夹角为α.如果线段AB关于l1的轴对称图形是A′B′,而A′B′关于l2的轴对称图形是A″B″.试问AB和A″B″间有什么关系?(见图)
设直线l1和直线l2相交,交点为O,其夹角为α.如果线段AB关于l1的轴对称图形是A′B′,而A′B′关于l2的轴对称图形是A″B″.试问AB和A″B″间有什么关系?(见图)
解:因为已知AB关于l1的对称图形是A′B′,A′B′关于l2的对称图形是A″B″,
所以AB=A′B′,A′B′=A″B″,
所以AB=A″B″,①
由于∠AOP=∠A′OP,∠A′OP′=∠A″OP′,
所以∠AOA″=2∠POP′=2α.
同理∠BOB″=2∠POP′=2α,
所以∠AOA″=∠BOB″=2α.②
由①,②可知:在平面上,如果两条直线相交,一个图形以这两条直线为对称轴,连续作两次对称移动,那么相当于这个图形以这两条直线的交点为旋转中心,以这两条直线的交角的2倍为旋转角,作了一个旋转移动,在旋转移动下,图形的大小不变.
分析:因为AB关于l1的对称图形是A′B′,A′B′关于l2的对称图形是A″B″,所以AB=A′B′,A′B′=A″B″,所以AB=A″B″.
点评:本题考查了在平面上,如果两条直线相交,一个图形以这两条直线为对称轴,连续作两次对称移动,那么相当于这个图形以这两条直线的交点为旋转中心,以这两条直线的交角的2倍为旋转角,作了一个旋转移动,在旋转移动下,图形的大小不变这一性质.
所以AB=A′B′,A′B′=A″B″,
所以AB=A″B″,①
由于∠AOP=∠A′OP,∠A′OP′=∠A″OP′,
所以∠AOA″=2∠POP′=2α.
同理∠BOB″=2∠POP′=2α,
所以∠AOA″=∠BOB″=2α.②
由①,②可知:在平面上,如果两条直线相交,一个图形以这两条直线为对称轴,连续作两次对称移动,那么相当于这个图形以这两条直线的交点为旋转中心,以这两条直线的交角的2倍为旋转角,作了一个旋转移动,在旋转移动下,图形的大小不变.
分析:因为AB关于l1的对称图形是A′B′,A′B′关于l2的对称图形是A″B″,所以AB=A′B′,A′B′=A″B″,所以AB=A″B″.
点评:本题考查了在平面上,如果两条直线相交,一个图形以这两条直线为对称轴,连续作两次对称移动,那么相当于这个图形以这两条直线的交点为旋转中心,以这两条直线的交角的2倍为旋转角,作了一个旋转移动,在旋转移动下,图形的大小不变这一性质.

练习册系列答案
相关题目
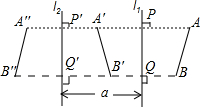
 2、设直线l1和直线l2平行,且l1和l2间的距离为a.如果线段AB在l1的右侧,并设AB关于l1的对称图形是A′B′,而A′B′关于l2的对称图形是A″B″(如图),那么,线段AB和A″B″有什么关系?
2、设直线l1和直线l2平行,且l1和l2间的距离为a.如果线段AB在l1的右侧,并设AB关于l1的对称图形是A′B′,而A′B′关于l2的对称图形是A″B″(如图),那么,线段AB和A″B″有什么关系?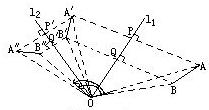 3、设直线l1和直线l2相交,交点为O,其夹角为α.如果线段AB关于l1的轴对称图形是A′B′,而A′B′关于l2的轴对称图形是A″B″.试问AB和A″B″间有什么关系?(见图)
3、设直线l1和直线l2相交,交点为O,其夹角为α.如果线段AB关于l1的轴对称图形是A′B′,而A′B′关于l2的轴对称图形是A″B″.试问AB和A″B″间有什么关系?(见图)