题目内容
【题目】AC是ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
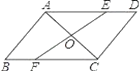
(1)求证:AE=CF;
(2)连接AF,CE.
①当EF和AC满足条件 时,四边形AFCE是菱形;
②若AB=1,BC=2,∠B=60°,则四边形AFCE为矩形时,EF的长是 .
【答案】(1)证明见解析;(2)①EF⊥AC,理由见解析;②![]()
【解析】试题分析:(1)由平行四边形的性质可知OA=OC,∠AEO=∠OFC,∠EAO=∠OCF,证出△AOE≌△COF,即可得出AE=CF.
(2)①先证明四边形AFCE是平行四边形,由EF⊥AC,即可得出四边形AFCE是菱形;②由矩形的性质得出EF=AC,∠AFB=∠AFC=90°,求出AF、CF,由勾股定理求出AC,即可得出EF的长.
试题解析:(1)证明:∵AD∥BC,
∴∠EAO=∠FCO.
∵O是AC的中点,
∴OA=OC,
在△AOE和△COF中,
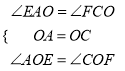 ,
,
∴△AOE≌△COF(ASA).
∴AE=CF.
(2)①当EF和AC满足条件EF⊥AC时,四边形AFCE是菱形;理由如下:如图所示:
∵AE∥CF,AE=CF,
∴四边形AFCE是平行四边形,
又∵EF⊥AC,
∴四边形AFCE是菱形;
②若四边形AFCE为矩形,
则EF=AC,∠AFB=∠AFC=90°,
∵AB=1,BC=2,∠B=60°,
∴∠BAF=30°,
∴BF=![]() AB=
AB=![]() ,
,
∴AF=![]() BF=
BF=![]() ,CF=2
,CF=2![]() =
=![]() ,
,
∴AC=![]() =
=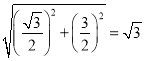 ,
,
∴EF=![]() ;
;
故答案为: ![]()

【题目】若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
| … | -4 | -3 | -2 | -1 | 0 | … |
| … | -5 | 0 | 3 | 4 | 3 | … |
(1)求此二次函数的表达式;
(2)画出此函数图象(不用列表).
(3)结合函数图象,当-4<x≤1时,写出y的取值范围.

【题目】如图1,在△ABC中,OB、OC是∠ABC、∠ACB的角平分线;
(1)填写下面的表格.
∠A的度数 | 50° | 60° | 70° |
∠BOC的度数 |
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想;
(3)如图2,△ABC的高BE、CD交于O点,试说明图中∠A与∠BOD的关系.



