题目内容
【题目】如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了![]() km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的什么方向上.
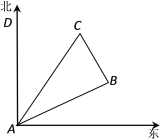
【答案】(1)10km;(2)点C在点A的北偏东30°的方向上
【解析】试题分析: (1)根据所走的方向可判断出△ABC是直角三角形,根据勾股定理可求出解.
(2)求出∠DAC的度数,即可求出方向.
试题解析:
(1)过B点作直线EF∥AD,
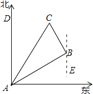
∴∠DAB=∠ABF=60°,
∵∠EBC=30°,
∴∠ABC =180°―∠ABF―∠EBC= 180°―60°―30°=90°,
∴ △ABC为直角三角形,由已知可得:BC=5km,AB=![]() km,
km,
由勾股定理可得:AC2=BC2+AB2,
所以AC=![]() =10(km),
=10(km),
即:A、C两点之间的距离为10km
(2)在Rt△ABC中, ∵BC=5km,AC=10km,∴∠CAB=30°,
∵∠DAB=60°,∴∠DAC=30°,
即点C在点A的北偏东30°的方向上.
点睛;勾股定理本身就是数形结合的一个典范,它把直角三角形有一个直角的“形”的特点,转化为三边“数”的关系,利用勾股定理解决实际问题,关键是利用数形结合思想将实际问题转化为直角三角形模型,再利用方程来解决.

练习册系列答案
相关题目