Question

【题目】已知关于的不等式组整数解为1、2，如果把适合这个不等式组的整数组成有序数对，那么对应在平面直角坐标系上的点共有的个数为_______．

Answer 1

【答案】6个

【解析】

首先解不等式组，不等式组的解集即可利用a，b表示，根据不等式组的整数解为1，2，即可确定a，b的范围，即可确定a，b的整数解，即可求解．

解：，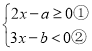

由①得：x≥，

由②得：x＜，

∴不等式组的解集为：≤x＜，

∵整数解有1，2，

在数轴上画出这个不等式组解集的可能区域，如下图

根据数轴可得：0＜≤1，2＜≤3，

由0＜≤1，得0＜a≤2，

∴a=1，2，共2个，

由2＜≤3，得6＜b≤9，

∴b=7，8，9，共3个，

2×3=6（个）．
故适合这个不等式组的整数a，b的有序数对（a，b）共有6个．
故答案为6个．