题目内容
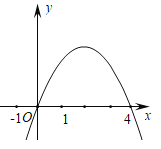
【题目】如图所示,一元二次方程x2+2x-3=0的两根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点C,B的横坐标,且此抛物线过点A(3,6)
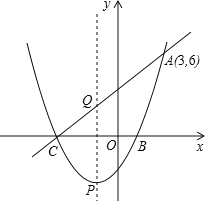
(1)求此抛物线的函数解析式;
(2)设此抛物线的顶点为P,对称轴与线段AC交于点Q,求点P,Q的坐标.
(3)在x轴上是否存在以动点M,使MQ+MA有最小值,若存在求出点M的坐标和最小值,若不存在,请说明理由.
【答案】(1)![]() ;(2)P(﹣1,﹣2),Q(﹣1,2);(3)存在,MQ+MA的最小值为
;(2)P(﹣1,﹣2),Q(﹣1,2);(3)存在,MQ+MA的最小值为![]() .
.
【解析】
(1)先求解方程x2+2x-3=0,得到B,C两点坐标,再设出抛物线的解析式为y=a(x+3)(x﹣1),再将点A(3,6)代入求解即可;
(2)将抛物线解析式化为顶点式得到P点坐标,设直线AC的解析式为y=kx+b,将A,C两点坐标代入得到直线AC的解析式,然后即可求得Q点坐标;
(3)连接AP,与x轴的交点即为所求点M,连接QM,根据点P,Q关于x轴对称,可得此时QM+AM=PM+AM为最小值,设直线AP的解析式为y=ax+c,利用待定系数法求求得直线AP的解析式,得到M点坐标为(0,0),过点A向PQ作垂线,垂足为H,在Rt△AHP中,利用勾股定理即可求得PA的值.
解:(1)解方程x2+2x-3=0,得x1=﹣3,x2=1,
∴交点C(﹣3,0),B(1,0),
设抛物线解析式为y=a(x+3)(x﹣1),
∵点A(3,6)在抛物线上,
∴解得a=![]() ,
,
则抛物线的函数解析式为![]() ;
;
(2)∵![]() ,
,
∴顶点P的坐标为(﹣1,﹣2),对称轴为直线x=﹣1,
设直线AC的解析式为y=kx+b,
∵A(3,6),C(﹣3,0)在直线AC上,
∴![]() ,
,
解得:k=1,b=3,
∴直线AC的解析式为:y=x+3,
当x=﹣1时,y=﹣1+3=2,
∴Q点坐标为(﹣1,2);
(3)存在,理由如下,
∵点P与点Q横坐标相等,纵坐标互为相反数,
∴点P,Q关于x轴对称,
∴连接AP,与x轴的交点即为所求点M,连接QM,
∴QM=PM,
∴QM+AM=PM+AM,
设直线AP的解析式为y=ax+c,
将A(3,6),P(﹣1,﹣2)代入y=ax+c得:
![]() ,
,
解得得a=2,c=0,
∴y=2x,
令y=0,则x=0,
∴点M的坐标为(0,0),
过点A向PQ作垂线,垂足为H,
则AH=4,PH=8,
在Rt△AHP中,![]() ,
,
∴MQ+MA=![]() .
.